Pruebas de Hipótesis

5. Pruebas de Hipótesis#

5.1. Test sobre una y dos muestras#

Se introducen dos funciones: stats.ttest_1samp y stats.wilcoxon para el test t y el test de Wilcoxon respectivamente. Ambos pueden ser usados para una muestra o dos muestras así como para datos pareados. Note que el test de Wilcoxon para dos muestras es lo mismo que el test de Mann–Whitney.

5.1.1. El test t#

Este test se basa en el supuesto de normalidad de los datos. Es decir que los datos \(x_1\ldots,x_n\) se asumen como realizaciones independientes de variables aleatorias con media \(\mu\) y varianza \(\sigma^2\), \(N(\mu, \sigma^2)\). Se tiene que la hipótesis nula es que \(\mu=\mu_0\).

Se puede estimar los parámetros \(\mu\) y \(\sigma\) por la media \(\bar{x}\) y la desviación estándar \(\sigma\), aunque recuerde que solo son estimaciones del valor real.

Veamos un ejemplo del consuo diario de calorías de 11 mujeres:

daily_intake = [5260,5470,5640,6180,6390,6515,
                  6805,7515,7515,8230,8770]

Veamos algunas estadísticas de resumen:

from scipy import stats
import numpy as np
stats.describe(daily_intake)

DescribeResult(nobs=11, minmax=(5260, 8770), mean=6753.636363636364, variance=1304445.4545454548, skewness=0.3674679616524392, kurtosis=-0.9757942883536157)

Se podría querer saber si el consumo de energía de las mujeres se desvía de una valor recomendado de \(7725\). Asumiendo que los datos vienen de una distribución normal, el objetivo es hacer una prueba para saber si la media de la distribución es \(\mu = 7725\).

stats.ttest_1samp(daily_intake,7725)

TtestResult(statistic=-2.8207540608310193, pvalue=0.018137235176105805, df=10)

t, pval = stats.ttest_1samp(daily_intake,7725)

t

-2.8207540608310193

pval

0.018137235176105805

5.1.2. Wilcoxon#

(rank, pVal) = stats.wilcoxon(x=(np.array(daily_intake)-7725))

(rank, pVal)

(8.0, 0.0244140625)

Para efectos prácticos, cuando se trata de una muestra, el test t y el de Wilcoxon suelen arrojar resultados muy similares.

5.2. Test t para dos muestras#

Se usa esta prueba con la hipótesis nula de que dos muestras provengan de distribuciones normales con la misma media.

Se puede tener dos enfoques, que las muestras tengan la misma varianza (enfoque clásico) o difieran en varianza.

import numpy as np
from scipy import stats
import pandas as pd
uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/energy.csv"
energy = pd.read_csv(uu)
energy.head()
expend stature
0 9.21 obese
1 7.53 lean
2 7.48 lean
3 8.08 lean
4 8.09 lean 
g1 = energy[energy.stature=='obese'].expend.values
g2 = energy[energy.stature=='lean'].expend.values
stats.ttest_ind(g2,g1,equal_var=False)

TtestResult(statistic=-3.855503558973697, pvalue=0.0014106918447179043, df=15.91873619676766)

stats.ttest_ind(g2,g1,equal_var=True)

TtestResult(statistic=-3.9455649161549835, pvalue=0.0007989982111700593, df=20.0)

5.2.1. Comparación de varianzas#

Aún cuando en python se puede hacer la prueba sobre dos muestras sin el supuesto de igualdad en las varianzas, podrías estar interesado en hacer una prueba exclusiva de este supuesto.

import statistics 
F = statistics.variance(g2)/statistics.variance(g1)
df1 = len(g1) - 1
df2 = len(g2) - 1
alpha = 0.05 
p_value = stats.f.cdf(F, df2, df1)
(F,p_value*2)

(0.7844459792357035, 0.6797459853760682)

5.2.2. Test de Wilcoxon para dos muestras#

u_statistic, pVal = stats.mannwhitneyu(g1, g2)

(u_statistic, pVal*2)

(105.0, 0.004243226771760096)

5.3. KS Test#

Compara la distribución subyacente de dos muestras independientes \(F(x)\) y \(G(x)\). Es válidas solo para distribuciones continuas.

stats.kstest(g1,g2)

KstestResult(statistic=0.8461538461538461, pvalue=0.00026536930561698365, statistic_location=8.4, statistic_sign=-1)

stats.kstest(g1,stats.norm.cdf)

KstestResult(statistic=1.0, pvalue=0.0, statistic_location=8.79, statistic_sign=-1)

stats.kstest(g2,stats.norm.cdf)

KstestResult(statistic=0.9999999995606046, pvalue=4.5514700442308465e-122, statistic_location=6.13, statistic_sign=-1)

5.4. Correlación#

Se aborda a continuación medidas de correlación paramétricas y no paramétricas. El coeficiente de correlación es una medida de asociación que varía entre -1 y 1.

5.4.1. Correlación de Pearson#

El coeficiente de correlación empírico es:

\[ r = \frac{\sum (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum (x_i-\bar{x})^2\sum (y_i-\bar{y})^2}} \]

La función cor en python calcula la correlación entre dos o más vectores.

uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/company_sales_data.csv"
import pandas as pd
datos = pd.read_csv(uu)

---------------------------------------------------------------------------
HTTPError                                 Traceback (most recent call last)
Cell In[18], line 3
      1 uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/company_sales_data.csv"
      2 import pandas as pd
----> 3 datos = pd.read_csv(uu)

File /opt/anaconda3/lib/python3.12/site-packages/pandas/io/parsers/readers.py:1026, in read_csv(filepath_or_buffer, sep, delimiter, header, names, index_col, usecols, dtype, engine, converters, true_values, false_values, skipinitialspace, skiprows, skipfooter, nrows, na_values, keep_default_na, na_filter, verbose, skip_blank_lines, parse_dates, infer_datetime_format, keep_date_col, date_parser, date_format, dayfirst, cache_dates, iterator, chunksize, compression, thousands, decimal, lineterminator, quotechar, quoting, doublequote, escapechar, comment, encoding, encoding_errors, dialect, on_bad_lines, delim_whitespace, low_memory, memory_map, float_precision, storage_options, dtype_backend)
   1013 kwds_defaults = _refine_defaults_read(
   1014     dialect,
   1015     delimiter,
   (...)
   1022     dtype_backend=dtype_backend,
   1023 )
   1024 kwds.update(kwds_defaults)
-> 1026 return _read(filepath_or_buffer, kwds)

File /opt/anaconda3/lib/python3.12/site-packages/pandas/io/parsers/readers.py:620, in _read(filepath_or_buffer, kwds)
    617 _validate_names(kwds.get("names", None))
    619 # Create the parser.
--> 620 parser = TextFileReader(filepath_or_buffer, **kwds)
    622 if chunksize or iterator:
    623     return parser

File /opt/anaconda3/lib/python3.12/site-packages/pandas/io/parsers/readers.py:1620, in TextFileReader.__init__(self, f, engine, **kwds)
   1617     self.options["has_index_names"] = kwds["has_index_names"]
   1619 self.handles: IOHandles | None = None
-> 1620 self._engine = self._make_engine(f, self.engine)

File /opt/anaconda3/lib/python3.12/site-packages/pandas/io/parsers/readers.py:1880, in TextFileReader._make_engine(self, f, engine)
   1878     if "b" not in mode:
   1879         mode += "b"
-> 1880 self.handles = get_handle(
   1881     f,
   1882     mode,
   1883     encoding=self.options.get("encoding", None),
   1884     compression=self.options.get("compression", None),
   1885     memory_map=self.options.get("memory_map", False),
   1886     is_text=is_text,
   1887     errors=self.options.get("encoding_errors", "strict"),
   1888     storage_options=self.options.get("storage_options", None),
   1889 )
   1890 assert self.handles is not None
   1891 f = self.handles.handle

File /opt/anaconda3/lib/python3.12/site-packages/pandas/io/common.py:728, in get_handle(path_or_buf, mode, encoding, compression, memory_map, is_text, errors, storage_options)
    725     codecs.lookup_error(errors)
    727 # open URLs
--> 728 ioargs = _get_filepath_or_buffer(
    729     path_or_buf,
    730     encoding=encoding,
    731     compression=compression,
    732     mode=mode,
    733     storage_options=storage_options,
    734 )
    736 handle = ioargs.filepath_or_buffer
    737 handles: list[BaseBuffer]

File /opt/anaconda3/lib/python3.12/site-packages/pandas/io/common.py:384, in _get_filepath_or_buffer(filepath_or_buffer, encoding, compression, mode, storage_options)
    382 # assuming storage_options is to be interpreted as headers
    383 req_info = urllib.request.Request(filepath_or_buffer, headers=storage_options)
--> 384 with urlopen(req_info) as req:
    385     content_encoding = req.headers.get("Content-Encoding", None)
    386     if content_encoding == "gzip":
    387         # Override compression based on Content-Encoding header

File /opt/anaconda3/lib/python3.12/site-packages/pandas/io/common.py:289, in urlopen(*args, **kwargs)
    283 """
    284 Lazy-import wrapper for stdlib urlopen, as that imports a big chunk of
    285 the stdlib.
    286 """
    287 import urllib.request
--> 289 return urllib.request.urlopen(*args, **kwargs)

File /opt/anaconda3/lib/python3.12/urllib/request.py:215, in urlopen(url, data, timeout, cafile, capath, cadefault, context)
    213 else:
    214     opener = _opener
--> 215 return opener.open(url, data, timeout)

File /opt/anaconda3/lib/python3.12/urllib/request.py:521, in OpenerDirector.open(self, fullurl, data, timeout)
    519 for processor in self.process_response.get(protocol, []):
    520     meth = getattr(processor, meth_name)
--> 521     response = meth(req, response)
    523 return response

File /opt/anaconda3/lib/python3.12/urllib/request.py:630, in HTTPErrorProcessor.http_response(self, request, response)
    627 # According to RFC 2616, "2xx" code indicates that the client's
    628 # request was successfully received, understood, and accepted.
    629 if not (200 <= code < 300):
--> 630     response = self.parent.error(
    631         'http', request, response, code, msg, hdrs)
    633 return response

File /opt/anaconda3/lib/python3.12/urllib/request.py:559, in OpenerDirector.error(self, proto, *args)
    557 if http_err:
    558     args = (dict, 'default', 'http_error_default') + orig_args
--> 559     return self._call_chain(*args)

File /opt/anaconda3/lib/python3.12/urllib/request.py:492, in OpenerDirector._call_chain(self, chain, kind, meth_name, *args)
    490 for handler in handlers:
    491     func = getattr(handler, meth_name)
--> 492     result = func(*args)
    493     if result is not None:
    494         return result

File /opt/anaconda3/lib/python3.12/urllib/request.py:639, in HTTPDefaultErrorHandler.http_error_default(self, req, fp, code, msg, hdrs)
    638 def http_error_default(self, req, fp, code, msg, hdrs):
--> 639     raise HTTPError(req.full_url, code, msg, hdrs, fp)

HTTPError: HTTP Error 429: Too Many Requests

datos
month_number facecream facewash toothpaste bathingsoap shampoo moisturizer total_units total_profit
0 1 2500 1500 5200 9200 1200 1500 21100 211000
1 2 2630 1200 5100 6100 2100 1200 18330 183300
2 3 2140 1340 4550 9550 3550 1340 22470 224700
3 4 3400 1130 5870 8870 1870 1130 22270 222700
4 5 3600 1740 4560 7760 1560 1740 20960 209600
5 6 2760 1555 4890 7490 1890 1555 20140 201400
6 7 2980 1120 4780 8980 1780 1120 29550 295500
7 8 3700 1400 5860 9960 2860 1400 36140 361400
8 9 3540 1780 6100 8100 2100 1780 23400 234000
9 10 1990 1890 8300 10300 2300 1890 26670 266700
10 11 2340 2100 7300 13300 2400 2100 41280 412800
11 12 2900 1760 7400 14400 1800 1760 30020 300200 
datos.plot('shampoo','bathingsoap',kind = 'scatter')

<Axes: xlabel='shampoo', ylabel='bathingsoap'>
_images/cacaaf31e2d67d5936900fcdb04cbdaf6d173c6b7356eb60296915db044ae6b5.png 
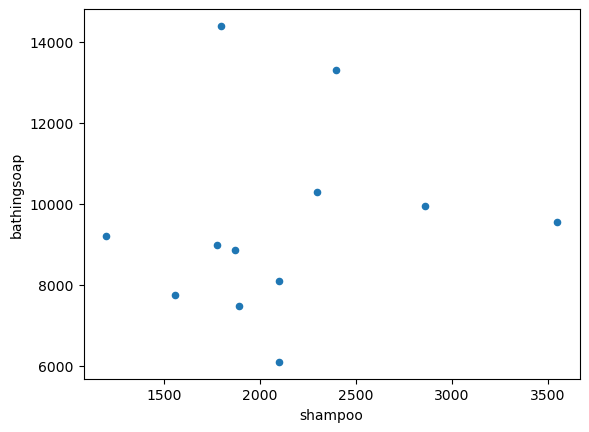
np.corrcoef(datos.shampoo,datos.bathingsoap)

array([[1.        , 0.13756757],
       [0.13756757, 1.        ]])

stats.pearsonr(datos.shampoo,datos.bathingsoap) # devuelve la correlacion y el p-valor

(0.1375675688230804, 0.669853167345746)

stats.spearmanr(datos.shampoo,datos.bathingsoap)   # Spearman's rho

SpearmanrResult(correlation=0.2907184843604137, pvalue=0.35929281767147814)

stats.kendalltau(datos.shampoo,datos.bathingsoap)  # Kendall's tau

KendalltauResult(correlation=0.10687334289668038, pvalue=0.6304167324095719)

Interpretación de la correlación:

  • La correlación esta siempre entre -1 y 1. Lo primero que se interpreta es el signo

  • Directamente proporcional si es positivo, si es negativo pasa lo contrario

  • En segundo lugar se interpreta es la fuerza de la relación. Si esta más cerca de 1, significa que si aumenta una variable, la otra también.

  • Números intermedios, reducen la fuerza de la relación.

Contents