8. Análisis de Componentes Principales#

8.1. Planteamiento1#

Se aplica a tablas de datos donde las filas son considerados como individuos y las columnas como datos cuantitativos.

Más formalmente, se dispone de los valores de \(p\) variables y \(n\) elementos dispuestos en una matriz \(\mathbf{X}\) de dimensión \(n\times p\).

Siempre (casi) se usa la matriz centrada y/o estandarizada, los paquetes suelen hacer este trabajo por nosostros. Supongamos que \(\mathbf{X}\) ha sido centrada, su matriz de varianza covarianza viene dada por \(\frac{1}{n}\mathbf{X'X}\).

¿Cómo encontrar un espacio de dimensión más reducida que represente adeucadamente los datos?

8.1.1. Notación#

Se desea encontrar un subespacio de dimensión menor que \(p\) tal que al proyectar sobre él los puntos conserven su estructura con la menor distorsión posible.

Consideremos primero un subespacio de dimensión uno (una recta) obtenida por un conjunto de \(p=2\) variables.

La siguiente figura indica el diagrama de dispersión y una recta que, intuitivamente, proporciona un buen resumen de los datos, ya que las proyecciones de los puntos sobre ella indican aproximadamente la situación de los puntos en el plano.

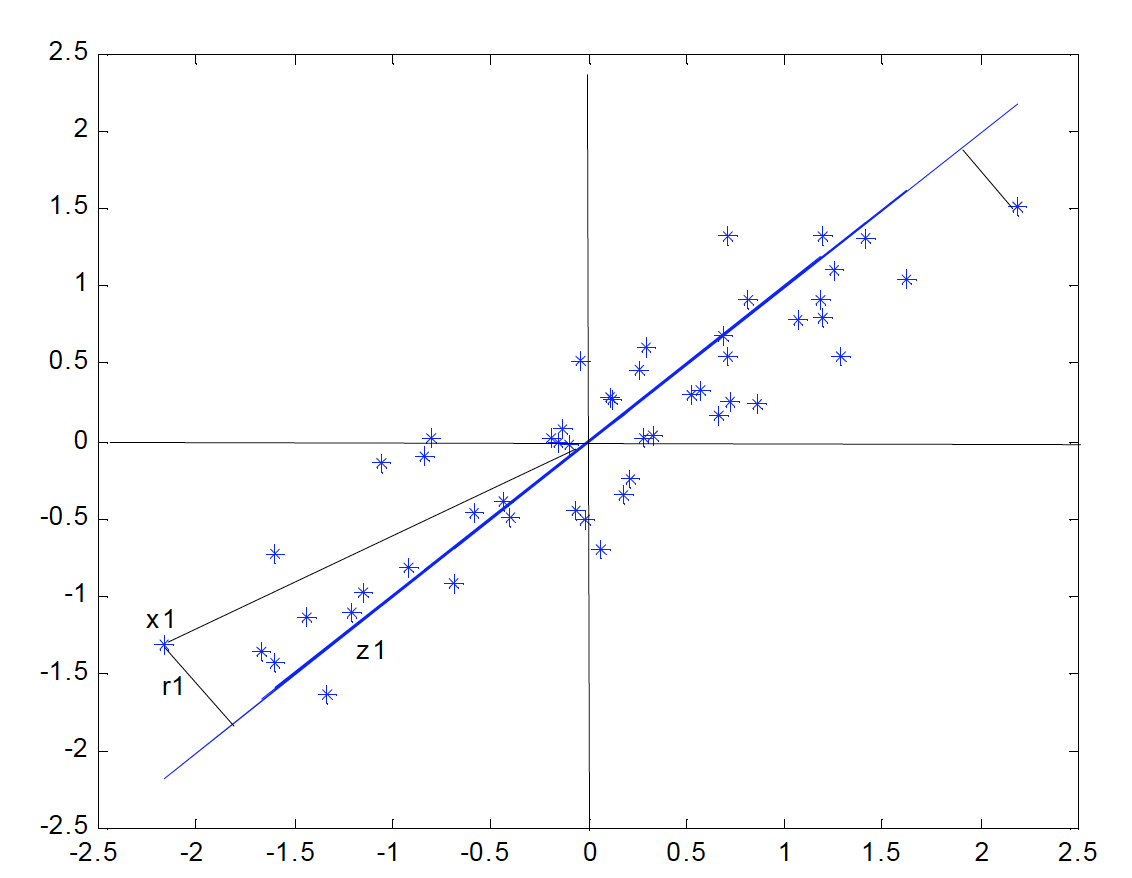
_images/fig1.png

Si consideramos un punto \(\mathbf{x_i}\) y una dirección \(\mathbf{a_1} = (a_{11}, \ldots, a_{1p})'\), definida por un vector \(\mathbf{a_1}\) de norma unidad, la proyección del punto \(\mathbf{x_i}\) sobre esta dirección es el escalar:

\[ z_i= a_{11}x_{i1}+\ldots+a_{1p}x_{ip} = \mathbf{a_1^{'}x_i} \]

y el vector que representa esta proyección será \(z_i\mathbf{a_1}\). Llamando \(r_i\) a la distancia entre el punto \(x_i\), y su proyección sobre la dirección \(\mathbf{a_1}\), este criterio implica:

\[ min\sum_{i = 1}^{n} r^2_i = \sum_{i = 1}^{n} |\mathbf{x_i}-z_i\mathbf{a_1}|^2 \]

donde \(|\cdot|\) es la norma euclideana o módulo del vector.

Notemos que al proyectar cada punto sobre la recta se forma un triángulo rectángulo donde la hipotenusa es la distancia al origen del punto al origen, \((\mathbf{x_i'x_i})^{1/2}\), y los catetos la proyeccion del punto sobre la recta \((z_i)\) y la distancia entre el punto y su proyección \((r_i)\). Por el teorema de Pitágoras, podemos escribir:

\[ (\mathbf{x_i'x_i}) = z_i^2+r_i^2 \]

y sumando esta expresión para todos los puntos, se obtiene:

\[ \sum_{i=1}^{n}(\mathbf{x_i'x_i}) = \sum_{i=1}^{n}z_i^2+\sum_{i=1}^{n}r_i^2 \]

Como el primer miembro es constante, minimizar \(\sum_{i=1}^{n}r_i^2\), la suma de las distancias a la recta de todos los puntos, es equivalente a maximizar \(\sum_{i=1}^{n}z_i^2\), la suma al cuadrado de los valores de las proyecciones. Como las proyecciones \(z_i\) son variables de media cero, maximizar la suma de sus cuadrados equivale a mazimizar su varianza.

¿Cómo es eso posible?

8.1.2. Cálculo del primer componente#

El primer componente principal será la combinación lineal de las variables originales que tenga varianza máxima. Los valores de este primer componente en los \(n\) individuos se representarán por un vector \(\mathbf{z_1}\), dado por

\[ \mathbf{z_1} = \mathbf{Xa_1} \]

Como las variables originales tienen media cero también \(\mathbf{z_1}\) tendrá media nula. Su varianza será:

\[ Var(\mathbf{z_1}) = \frac{1}{n}\mathbf{z_1^{'}z_1} = \frac{1}{n}\mathbf{a_1^{'}X'Xa_1} = \mathbf{a_1^{'}Sa_1} \]

donde \(S\) es la matriz de varianzas y covarianzas de las observaciones. Para que la maximización de la ecuación anterior tenga solución debemos imponer una restricción al módulo del vector \(\mathbf{a_1}\), y, sin pérdida de generalidad, impondremos que \(\mathbf{a_1^{'}a_1}=1\). Usamos para ello el multiplicador de Lagrange

\[ M = \mathbf{a_1^{'}Sa_1}- \lambda(\mathbf{a_1^{'}a_1}-1) \]

Se maximiza derivando respecto a los componentes de \(\mathbf{a_1}\) e igualando a cero. Entonces

\[ \frac{\partial M}{\partial\mathbf{a_1}} = 2\mathbf{Sa_1}-2\lambda\mathbf{a_1} = 0 \]

cuya solución es:

\[ \mathbf{Sa_1} = \lambda\mathbf{a_1} \]

que implica que \(\mathbf{a1}\) es un vector propio de la matriz \(\mathbf{S}\), y \(\lambda\) su correspondiente valor propio. Para determinar qué valor propio de \(\mathbf{S}\) es la solución de la ecuación tendremos en cuenta que, multiplicando por la izquierda por \(\mathbf{a'_{1}}\) esta ecuación,

\[ \mathbf{a_1^{'}Sa_1} = \lambda \mathbf{a_1^{'}a_1} = \lambda \]

y concluimos, que \(\lambda\) es la varianza de \(\mathbf{z_1}\). Como esta es la cantidad que queremos maximizar, \(\lambda\) será el mayor valor propio de la matriz \(\mathbf{S}\). Su vector asociado, \(\mathbf{a1}\), define los coeficientes de cada variable en el primer componente principal.

Ejemplo

El siguiente conjunto de datos corresponde a calificaciones de 20 estudiantes en 5 materias Ciencias Natuales (CNa), Matemáticas (Mat), Francés (Fra), Latín (Lat) y Literatura (Lit)

import pandas as pd
import seaborn as sns
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt

CNa = [7,5,5,6,7,4,5,5,6,6,6,5,6,8,6,4,6,6,6,7]
Mat = [7,5,6,8,6,4,5,6,5,5,7,5,6,7,7,3,4,6,5,7]
Fra = [5,6,5,5,6,6,5,5,7,6,5,4,6,8,5,4,7,7,4,6]
Lat = [5,6,7,6,7,7,5,5,6,6,6,5,6,8,6,4,8,7,4,7]
Lit = [6,5,5,6,6,6,6,5,6,6,5,4,5,8,6,4,7,7,4,6]
Notas = pd.DataFrame({'CNa':CNa,'Mat':Mat,'Fra':Fra,'Lat':Lat,'Lit':Lit})
Notas
CNa Mat Fra Lat Lit
0 7 7 5 5 6
1 5 5 6 6 5
2 5 6 5 7 5
3 6 8 5 6 6
4 7 6 6 7 6
5 4 4 6 7 6
6 5 5 5 5 6
7 5 6 5 5 5
8 6 5 7 6 6
9 6 5 6 6 6
10 6 7 5 6 5
11 5 5 4 5 4
12 6 6 6 6 5
13 8 7 8 8 8
14 6 7 5 6 6
15 4 3 4 4 4
16 6 4 7 8 7
17 6 6 7 7 7
18 6 5 4 4 4
19 7 7 6 7 6

Es pertiente empezar por un análisis explotario para tener una mejor perspectiva de los datos:

Notas.describe()
CNa Mat Fra Lat Lit
count 20.000000 20.000000 20.000000 20.000000 20.00000
mean 5.800000 5.700000 5.600000 6.050000 5.65000
std 1.005249 1.260743 1.095445 1.145931 1.03999
min 4.000000 3.000000 4.000000 4.000000 4.00000
25% 5.000000 5.000000 5.000000 5.000000 5.00000
50% 6.000000 6.000000 5.500000 6.000000 6.00000
75% 6.000000 7.000000 6.000000 7.000000 6.00000
max 8.000000 8.000000 8.000000 8.000000 8.00000 
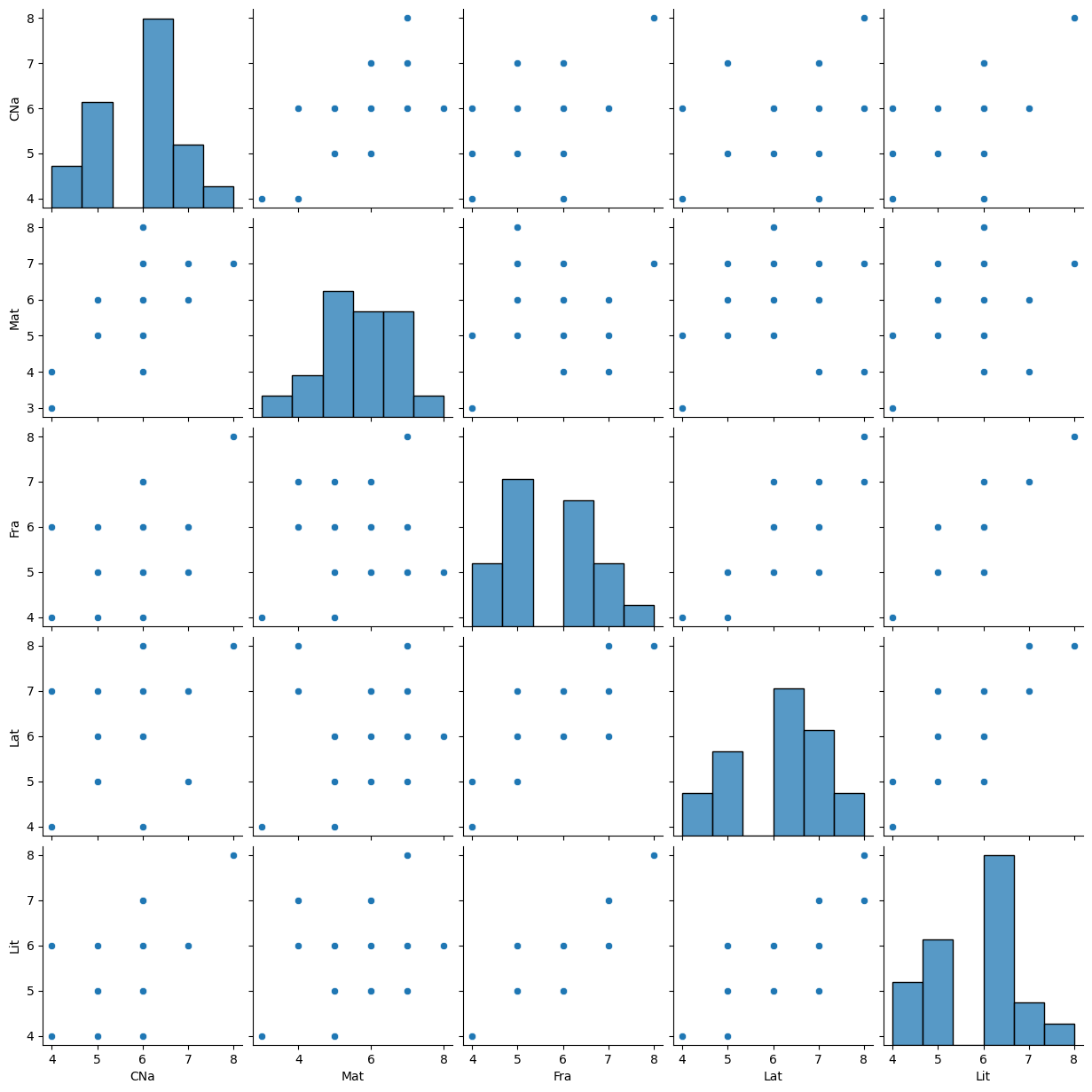
sns.pairplot(Notas)

<seaborn.axisgrid.PairGrid at 0x7f9ba66b6910>
_images/24e4a93a119b672cbb3a7705416b1df884e869c7caf81cdf0c2186ccd31c77d0.png

Como habíamos visto, los valores propios corresponden la varianzas explicadas de cada componente y los vectores propios son sus direcciones o pesos (loadings). Es decir:

print(np.corrcoef(Notas.T))

[[1.         0.6561498  0.49706742 0.42034118 0.58398469]
 [0.6561498  1.         0.09908375 0.2295101  0.31711567]
 [0.49706742 0.09908375 1.         0.81339038 0.84081035]
 [0.42034118 0.2295101  0.81339038 1.         0.76622848]
 [0.58398469 0.31711567 0.84081035 0.76622848 1.        ]]

def fc (x):
    val = x-np.mean(x)
    return(val)


Notasc = Notas.apply(fc)

from numpy import linalg as LA
from sklearn.decomposition import PCA
from IPython.display import display

S = np.cov(Notas.T) # Matriz de covarianza
e_values, e_vectors = LA.eig(S) # valores y vectores propios

print(e_values)
print(e_vectors)

[3.77855877 1.66135364 0.40960181 0.22023537 0.12498724]
[[-0.39534516 -0.33102922 -0.66155123  0.47595392  0.26446114]
 [-0.34882879 -0.79772358  0.37084614 -0.17998543 -0.2683914 ]
 [-0.48225721  0.37154122 -0.21520882 -0.01712248 -0.76339838]
 [-0.50400573  0.29871462  0.59983776  0.46491466  0.28424781]
 [-0.48520809  0.16365646 -0.13675863 -0.72431643  0.44096764]]

Ahora podemos calcular los puntajes de los componetes por individuo:

np.matmul(Notasc,e_vectors) #scores
0 1 2 3 4
0 -0.279154 -1.913571 -0.860331 -0.394234 0.282362
1 0.708139 0.850534 0.242466 0.185938 -0.629896
2 0.337562 -0.020016 1.428359 0.487989 0.149359
3 -0.736643 -2.081551 0.771904 -0.585259 0.033757
4 -1.420594 -0.146877 -0.246711 0.698458 0.355851
5 0.463099 2.441658 0.996251 -0.369433 0.099250
6 1.209194 0.343935 -0.278921 -0.986171 0.290223
7 1.345573 -0.617445 0.228684 -0.441840 -0.419136
8 -0.654672 1.054702 -0.771052 -0.079547 -0.687865
9 -0.172414 0.683161 -0.555843 -0.062425 0.075533
10 0.097393 -1.447484 0.537816 0.319043 -0.138819
11 2.661867 -0.354920 0.209805 0.479584 0.171686
12 -0.036035 -0.278219 -0.048239 0.481906 -0.633826
13 -4.603704 0.093480 -0.641513 -0.023536 -0.008693
14 -0.387815 -1.283827 0.401058 -0.405273 0.302149
15 4.258876 1.272842 -0.470174 -0.101313 0.159760
16 -1.799062 2.613512 -0.078982 0.305951 0.589989
17 -1.992714 0.719350 0.062873 -0.518935 -0.231041
18 2.770528 -0.984663 -1.051584 0.490624 0.151899
19 -1.769423 -0.944601 0.124135 0.518473 0.087459

El porcentaje de la varianza explicada por cada componente es:

(e_values/np.sum(e_values))

array([0.60996276, 0.26818793, 0.06612094, 0.03555201, 0.02017636])

Verifiquemos nuestros resultados usando python

pcaMod = PCA(n_components=5).fit(Notas)


pcaMod.explained_variance_ratio_

array([0.60996276, 0.26818793, 0.06612094, 0.03555201, 0.02017636])

pcaMod.components_ # Loadings

array([[ 0.39534516,  0.34882879,  0.48225721,  0.50400573,  0.48520809],
       [-0.33102922, -0.79772358,  0.37154122,  0.29871462,  0.16365646],
       [-0.66155123,  0.37084614, -0.21520882,  0.59983776, -0.13675863],
       [-0.47595392,  0.17998543,  0.01712248, -0.46491466,  0.72431643],
       [-0.26446114,  0.2683914 ,  0.76339838, -0.28424781, -0.44096764]])

scores = pcaMod.transform(Notas) # scores
scores

array([[ 0.27915411, -1.91357104, -0.86033137,  0.39423402, -0.28236204],
       [-0.70813894,  0.85053394,  0.24246638, -0.18593762,  0.62989564],
       [-0.33756163, -0.02001625,  1.42835911, -0.48798933, -0.14935915],
       [ 0.73664347, -2.08155078,  0.77190377,  0.5852587 , -0.03375732],
       [ 1.42059398, -0.146877  , -0.24671081, -0.69845826, -0.35585069],
       [-0.46309908,  2.44165783,  0.9962506 ,  0.36943263, -0.09925008],
       [-1.20919379,  0.34393456, -0.27892119,  0.98617099, -0.29022257],
       [-1.34557309, -0.61744548,  0.22868359,  0.44183999,  0.41913648],
       [ 0.65467152,  1.05470241, -0.77105231,  0.07954737,  0.68786524],
       [ 0.17241431,  0.68316118, -0.55584349,  0.06242489, -0.07553314],
       [-0.09739341, -1.44748367,  0.53781626, -0.31904316,  0.13881893],
       [-2.66186718, -0.35491959,  0.2098049 , -0.47958435, -0.17168566],
       [ 0.03603501, -0.27821886, -0.04823871, -0.48190611,  0.6338259 ],
       [ 4.60370426,  0.09348019, -0.64151305,  0.02353642,  0.00869323],
       [ 0.38781468, -1.2838272 ,  0.40105762,  0.40527327, -0.30214872],
       [-4.25887565,  1.27284218, -0.47017392,  0.10131336, -0.15975951],
       [ 1.79906227,  2.61351169, -0.07898156, -0.30595095, -0.58998944],
       [ 1.99271412,  0.71934991,  0.06287296,  0.51893457,  0.23104118],
       [-2.77052775, -0.98466343, -1.0515841 , -0.49062361, -0.15189898],
       [ 1.76942278, -0.94460058,  0.12413533, -0.51847283, -0.08745929]])

def pca_summary(pca, standardised_data, out=True):
    names = ["PC"+str(i) for i in range(1, len(pca.explained_variance_ratio_)+1)]
    a = list(np.std(pca.transform(standardised_data), axis=0))
    b = list(pca.explained_variance_ratio_)
    c = [np.sum(pca.explained_variance_ratio_[:i]) for i in range(1, len(pca.explained_variance_ratio_)+1)]
    columns = pd.MultiIndex.from_tuples([("sdev", "Standard deviation"), ("varprop", "Proportion of Variance"), ("cumprop", "Cumulative Proportion")])
    summary = pd.DataFrame(list(zip(a, b, c)), index=names, columns=columns)
    if out:
        print("Importance of components:")
        display(summary)
    return summary



sumpca = pca_summary(pcaMod, Notas)

Importance of components:
sdev varprop cumprop
Standard deviation Proportion of Variance Cumulative Proportion
PC1 1.894632 0.609963 0.609963
PC2 1.256299 0.268188 0.878151
PC3 0.623796 0.066121 0.944272
PC4 0.457410 0.035552 0.979824
PC5 0.344584 0.020176 1.000000 
def screeplot(pca, standardised_values):
    y = np.std(pca.transform(standardised_values), axis=0)**2
    x = np.arange(len(y)) + 1
    plt.plot(x, y, "o-")
    plt.xticks(x, ["Comp."+str(i) for i in x], rotation=60)
    plt.ylabel("Variance")
    plt.show()

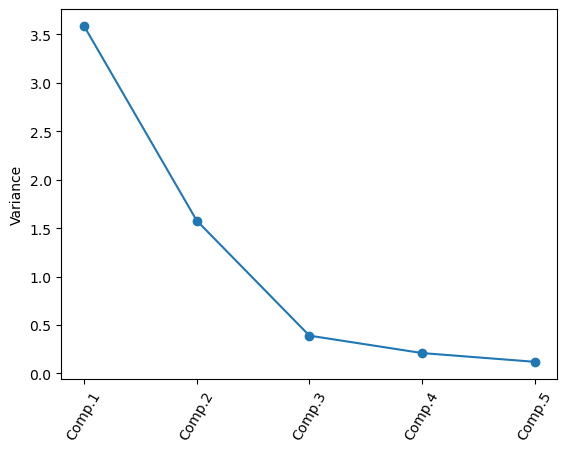
screeplot(pcaMod, Notas)
_images/69b3fb4230f2b29cebedd1978b737ba08b097a53b96d7cbff00c76451c6d51bc.png 
def biplot(score,coeff,labels=None):
    xs = score[:,0]
    ys = score[:,1]
    n = coeff.shape[0]
    scalex = 1.0/(xs.max() - xs.min())
    scaley = 1.0/(ys.max() - ys.min())
    plt.scatter(xs * scalex,ys * scaley)
    for i in range(n):
        plt.arrow(0, 0, coeff[i,0], coeff[i,1],color = 'r',alpha = 0.5)
        if labels is None:
            plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, "Var"+str(i+1), color = 'g', ha = 'center', va = 'center')
        else:
            plt.text(coeff[i,0]* 1.15, coeff[i,1] * 1.15, labels[i], color = 'g', ha = 'center', va = 'center')
    plt.xlim(-1,1)
    plt.ylim(-1,1)
    plt.xlabel("PC{}".format(1))
    plt.ylabel("PC{}".format(2))
    plt.grid()




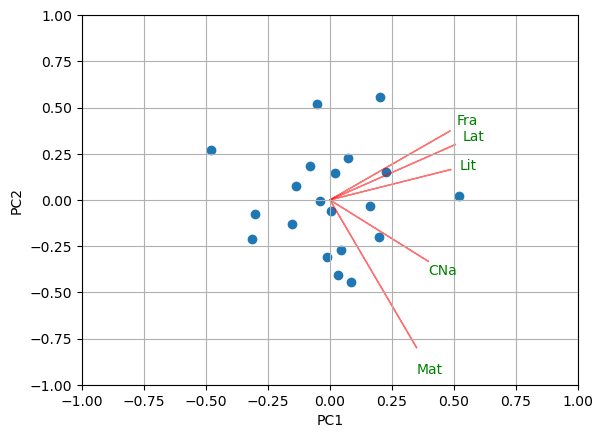
biplot(scores[:,0:2],np.transpose(pcaMod.components_[0:2, :]),labels = Notas.columns)
_images/7344ade9cedc27da91b1f834fa5f1f73b2a4cead49685ebf6548aa4bb0216bc3.png
1

Teoría obtenida de Peña, D. Análisis de datos multivariantes (2002). Referencias de FactoMineR vienen de Husson, F. Exploratory multivariate analysis by example using R (2017)