3. Gráficos básicos: matplotlib & seaborn

import matplotlib as mpl
mpl.get_backend()

'module://matplotlib_inline.backend_inline'

import matplotlib.pyplot as plt
plt.rcParams.update({'figure.max_open_warning': 0})
#plt.plot?

Dado que el estilo predeterminado es la línea ‘-’, no se mostrará nada si solo pasamos en un punto \((3,2)\)

plt.plot(3, 2)

[<matplotlib.lines.Line2D at 0x7fce03dc3280>]

Podemos pasarle ‘.’ a plt.plot para indicar que queremos el punto \((3,2)\) tal que sea puesto como un marker

plt.plot(3, 2, '.')

[<matplotlib.lines.Line2D at 0x7fce03df9ca0>]

Veamos como hacer un plot usando la capa scripting.

# Primero configuremos el backend sin usar mpl.use() de la capa de scripting
from matplotlib.backends.backend_agg import FigureCanvasAgg
from matplotlib.figure import Figure

# crear una nueva figura
fig = Figure()

# asociamos "fig" con el backend
canvas = FigureCanvasAgg(fig)

# se agrega un subplot a la figura
ax = fig.add_subplot(111)

# graficamos el punto (3,2)
ax.plot(3, 2, '.')

# guardamos la figura en test.png
#canvas.print_png('test.png')

[<matplotlib.lines.Line2D at 0x7fce04a365e0>]

# creamos una nueva figura
plt.figure()

# graficamos el punto (3,2) usando el marker de circulo
plt.plot(3, 2, 'o')

# obtenemos el eje actual
ax = plt.gca()

# Fijamos las propiedades del eje [xmin, xmax, ymin, ymax]
ax.axis([0,6,0,10])

(0.0, 6.0, 0.0, 10.0)

# creamos una nueva figura
plt.figure()

# graficamos el punto (1.5, 1.5) usando un marker de circulo
plt.plot(1.5, 1.5, 'o')
# graficamos el punto (2, 2) usando un marker de circulo
plt.plot(2, 2, 'o')
# graficamos el punto (2.5, 2.5) usando un marker de circulo
plt.plot(2.5, 2.5, 'o')

[<matplotlib.lines.Line2D at 0x7fce04be8eb0>]

# Accedemos al eje actual
ax = plt.gca()
# obtenemos todos los objetos hijo que contiene el eje
ax.get_children()

[<matplotlib.spines.Spine at 0x7fce04c2f3d0>,
 <matplotlib.spines.Spine at 0x7fce04c2f4c0>,
 <matplotlib.spines.Spine at 0x7fce04c2f5b0>,
 <matplotlib.spines.Spine at 0x7fce04c2f6a0>,
 <matplotlib.axis.XAxis at 0x7fce04c2f400>,
 <matplotlib.axis.YAxis at 0x7fce04c2fc10>,
 Text(0.5, 1.0, ''),
 Text(0.0, 1.0, ''),
 Text(1.0, 1.0, ''),
 <matplotlib.patches.Rectangle at 0x7fce04c3de80>]

3.1. Scatterplots

import numpy as np

x = np.array([1,2,3,4,5,6,7,8])
y = x

plt.figure()
plt.scatter(x, y) # similar a plt.plot(x, y, '.'), pero los objetos hijos en "axes" no son Line2D

<matplotlib.collections.PathCollection at 0x7fce04dc0880>

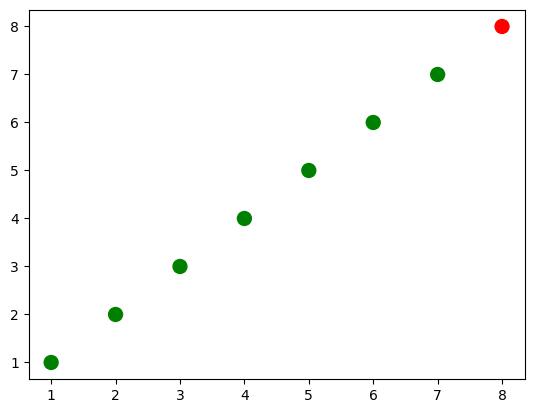
import numpy as np

x = np.array([1,2,3,4,5,6,7,8])
y = x

# creamos una lista de colores para cada punto que tenemos
# ['green', 'green', 'green', 'green', 'green', 'green', 'green', 'red']
colors = ['green']*(len(x)-1)
colors.append('red')

plt.figure()

# graficamos el punto con tamaño 100 y los colores elegidos
plt.scatter(x, y, s=100, c=colors)

<matplotlib.collections.PathCollection at 0x7fce05066280>

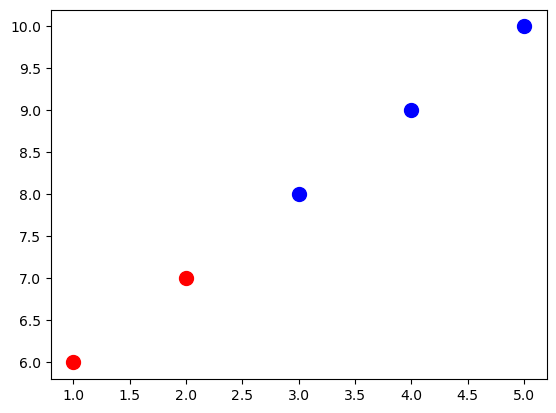
# convertimos las dos listas en una lista de tuplas en parejas
zip_generator = zip([1,2,3,4,5], [6,7,8,9,10])

print(list(zip_generator))
# lo de arriba imprime:
# [(1, 6), (2, 7), (3, 8), (4, 9), (5, 10)]

zip_generator = zip([1,2,3,4,5], [6,7,8,9,10])
# La estrella * "desempaca" una colección en argumentos posicionales
print(*zip_generator)
# lo de arriba imprime:
# (1, 6) (2, 7) (3, 8) (4, 9) (5, 10)

[(1, 6), (2, 7), (3, 8), (4, 9), (5, 10)]
(1, 6) (2, 7) (3, 8) (4, 9) (5, 10)

# use zip para convertir 5 tuplas con 2 elementos cada una en 2 tuplas con 5 elementos cada una
print(list(zip((1, 6), (2, 7), (3, 8), (4, 9), (5, 10))))
# lo de arriba imprime:
# [(1, 2, 3, 4, 5), (6, 7, 8, 9, 10)]


zip_generator = zip([1,2,3,4,5], [6,7,8,9,10])
# volvamos los datos a 2 listas
x, y = zip(*zip_generator) # Lo siguiente es equivalente zip((1, 6), (2, 7), (3, 8), (4, 9), (5, 10))
print(x)
print(y)
# lo de arriba imprime:
# (1, 2, 3, 4, 5)
# (6, 7, 8, 9, 10)

[(1, 2, 3, 4, 5), (6, 7, 8, 9, 10)]
(1, 2, 3, 4, 5)
(6, 7, 8, 9, 10)

plt.figure()
# graficar una serie de datos 'Estudiantes altos' en rojo usando los dos primeros elementos de x e y
plt.scatter(x[:2], y[:2], s=100, c='red', label='Estudiantes altos')
# graficamos una segunda serie de datos 'Estudiantes bajos' en azul usando los últimos tres elementos de x e y 
plt.scatter(x[2:], y[2:], s=100, c='blue', label='Estudiantes bajos')

<matplotlib.collections.PathCollection at 0x7fce048fd790>

# agregamos una etiqueta en el eje x
plt.xlabel('Número de veces que el niño patea una pelota')
# agregamos una etiqueta en el eje y
plt.ylabel('La nota del estudiante')
# add a title
plt.title('Relación entre patear la pelota y notas')

Text(0.5, 1.0, 'Relación entre patear la pelota y notas')

# agregar una leyenda (usa las etiquetas de plt.scatter)
plt.legend()

No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.

<matplotlib.legend.Legend at 0x7fce0534c490>

# agregue la leyenda a loc = 4 (la esquina inferior derecha), también elimina el marco y agrega un título
plt.legend(loc=4, frameon=False, title='Legenda')

No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.

<matplotlib.legend.Legend at 0x7fce055df670>

# obtener hijos de los ejes actuales (la leyenda es el penúltimo elemento de esta lista)
plt.gca().get_children()

[<matplotlib.spines.Spine at 0x7fce0573a910>,
 <matplotlib.spines.Spine at 0x7fce0573aa00>,
 <matplotlib.spines.Spine at 0x7fce0573aaf0>,
 <matplotlib.spines.Spine at 0x7fce0573abe0>,
 <matplotlib.axis.XAxis at 0x7fce0573a940>,
 <matplotlib.axis.YAxis at 0x7fce05744190>,
 Text(0.5, 1.0, ''),
 Text(0.0, 1.0, ''),
 Text(1.0, 1.0, ''),
 <matplotlib.patches.Rectangle at 0x7fce05755160>]

3.2. Gráficos de linea

import numpy as np

linear_data = np.array([1,2,3,4,5,6,7,8])
exponential_data = linear_data**2

plt.figure()
# graficar los datos lineales y los datos exponenciales
plt.plot(linear_data, '-o', exponential_data, '-o')

[<matplotlib.lines.Line2D at 0x7fce059e22b0>,
 <matplotlib.lines.Line2D at 0x7fce059e2370>]

# graficar otra serie con una línea roja discontinua
plt.plot([22,44,55], '--r')

[<matplotlib.lines.Line2D at 0x7fce05a843d0>]

plt.xlabel('Algún conjunto de datos')
plt.ylabel('Otro conjunto de datos')
plt.title('Un título')
# agregue una leyenda con entradas de leyenda (porque no teníamos etiquetas cuando graficamos la serie de datos)
plt.legend(['Línea base', 'Compentencia', 'Nosotros'])

<matplotlib.legend.Legend at 0x7fce05aa4dc0>

# llenar el área entre los datos lineales y los datos exponenciales
plt.gca().fill_between(range(len(linear_data)), 
                       linear_data, exponential_data, 
                       facecolor='blue', 
                       alpha=0.25)

<matplotlib.collections.PolyCollection at 0x7fce05e944c0>

¡Intentemos trabajar con fechas!

plt.figure()

observation_dates = np.arange('2017-01-01', '2017-01-09', dtype='datetime64[D]')

plt.plot(observation_dates, linear_data, '-o',  observation_dates, exponential_data, '-o')

[<matplotlib.lines.Line2D at 0x7fce05ee9760>,
 <matplotlib.lines.Line2D at 0x7fce05f36a60>]

Intentemos usar pandas

import pandas as pd
plt.figure()
observation_dates = np.arange('2017-01-01', '2017-01-09', dtype='datetime64[D]')
observation_dates = list(map(pd.to_datetime, observation_dates)) #convertir el map en una lista
plt.plot(observation_dates, linear_data, '-o',  observation_dates, exponential_data, '-o')

[<matplotlib.lines.Line2D at 0x7fce06fe2940>,
 <matplotlib.lines.Line2D at 0x7fce0700edc0>]

x = plt.gca().xaxis

# rotar las etiquetas del eje x
for item in x.get_ticklabels():
    item.set_rotation(45)

# ajustar el subplot para que el texto no se salga de la imagen
plt.subplots_adjust(bottom=0.25)

<Figure size 640x480 with 0 Axes>

ax = plt.gca()
ax.set_xlabel('Fecha')
ax.set_ylabel('Unidades')
ax.set_title('Rendimiento Exponencial vs. Lineal')

Text(0.5, 1.0, 'Rendimiento Exponencial vs. Lineal')

# you can add mathematical expressions in any text element
ax.set_title("Rendimiento Exponential ($x^2$) vs. Linear ($x$)")

Text(0.5, 1.0, 'Rendimiento Exponential ($x^2$) vs. Linear ($x$)')

3.3. Gráficos de barras

plt.figure()
xvals = range(len(linear_data))
plt.bar(xvals, linear_data, width = 0.3)

<BarContainer object of 8 artists>

new_xvals = []

# graficar otro conjunto de barras, ajustando los nuevos "xvals" para compensar el primer conjunto de barras graficados
for item in xvals:
    new_xvals.append(item+0.3)

plt.bar(new_xvals, exponential_data, width = 0.3 ,color='red')

<BarContainer object of 8 artists>

from random import randint
linear_err = [randint(0,15) for x in range(len(linear_data))] 

# Esto graficará un nuevo conjunto de barras con barras de error utilizando la lista de valores de error aleatorios.
plt.bar(xvals, linear_data, width = 0.3, yerr=linear_err)

<BarContainer object of 8 artists>

# También son posibles gráficos de barras apiladas
plt.figure()
xvals = range(len(linear_data))
plt.bar(xvals, linear_data, width = 0.3, color='b')
plt.bar(xvals, exponential_data, width = 0.3, bottom=linear_data, color='r')

<BarContainer object of 8 artists>

# o usar "barh" para gráficos de barras horizontales
plt.figure()
xvals = range(len(linear_data))
plt.barh(xvals, linear_data, height = 0.3, color='b')
plt.barh(xvals, exponential_data, height = 0.3, left=linear_data, color='r')

<BarContainer object of 8 artists>

3.4. Subplots

import matplotlib.pyplot as plt
import numpy as np

#plt.subplot?

plt.figure()
# el subplot con 1 fila, 2 columnas y el eje actual es el primer eje del subplot
plt.subplot(1, 2, 1)

linear_data = np.array([1,2,3,4,5,6,7,8])

plt.plot(linear_data, '-o')

[<matplotlib.lines.Line2D at 0x7fce07bab430>]

exponential_data = linear_data**2 

# el subplot con 1 fila, 2 columnas, y el eje actual es el segundo eje del subplot
plt.subplot(1, 2, 2)
plt.plot(exponential_data, '-o')

[<matplotlib.lines.Line2D at 0x7fce07d1b250>]

# graficar datos exponenciales en el primer eje
plt.subplot(1, 2, 1)
plt.plot(exponential_data, '-x')

[<matplotlib.lines.Line2D at 0x7fce07dcf8e0>]

plt.figure()
ax1 = plt.subplot(1, 2, 1)
plt.plot(linear_data, '-o')
# pasamos sharey = ax1 para asegurarse de que los dos subplots compartan el mismo eje y
ax2 = plt.subplot(1, 2, 2, sharey=ax1)
plt.plot(exponential_data, '-x')

[<matplotlib.lines.Line2D at 0x7fce07f35fa0>]

plt.figure()
# el lado derecho es una sintaxis abreviada equivalente
plt.subplot(1,2,1) == plt.subplot(121)

True

# creamos un grid 3x3 de subplots
fig, ((ax1,ax2,ax3), (ax4,ax5,ax6), (ax7,ax8,ax9)) = plt.subplots(3, 3, sharex=True, sharey=True)
# graficamos linear_data en el quinto eje del subplot
ax5.plot(linear_data, '-')

[<matplotlib.lines.Line2D at 0x7fce07b6fac0>]

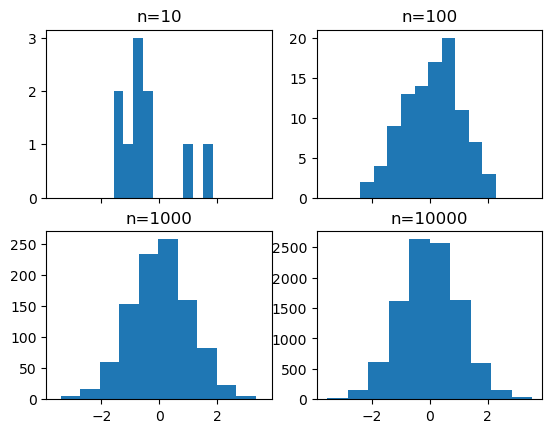
3.5. Histogramas

# creamos un grid 2x2 de subplots
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, sharex=True)
axs = [ax1,ax2,ax3,ax4]
import random 
random.seed(30)
# obtenemos muestras de n = 10, 100, 1000, y 10000 de uns distribución normal y graficamos los histogramas
for n in range(0,len(axs)):
    sample_size = 10**(n+1)
    sample = np.random.normal(loc=0.0, scale=1.0, size=sample_size)
    axs[n].hist(sample)
    axs[n].set_title('n={}'.format(sample_size))

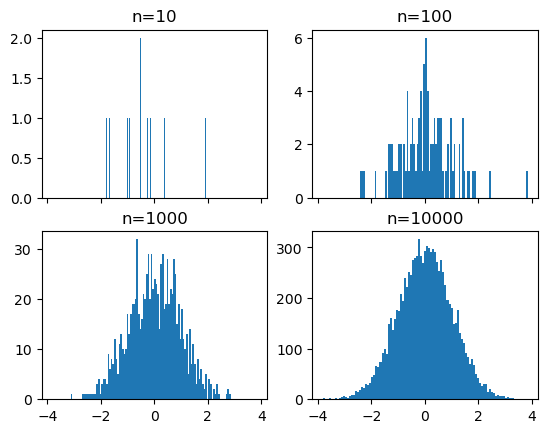
# repetimos con el numero de bins en 100
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, sharex=True)
axs = [ax1,ax2,ax3,ax4]

for n in range(0,len(axs)):
    sample_size = 10**(n+1)
    sample = np.random.normal(loc=0.0, scale=1.0, size=sample_size)
    axs[n].hist(sample, bins=100)
    axs[n].set_title('n={}'.format(sample_size))

plt.figure()
Y = np.random.normal(loc=0.0, scale=1.0, size=10000)
X = np.random.random(size=10000)
plt.scatter(X,Y)

<matplotlib.collections.PathCollection at 0x7fce0a0b5fd0>

# usamos gridspec para dividir la figura en subplots
import matplotlib.gridspec as gridspec

plt.figure()
gspec = gridspec.GridSpec(3, 3)

top_histogram = plt.subplot(gspec[0, 1:])
side_histogram = plt.subplot(gspec[1:, 0])
lower_right = plt.subplot(gspec[1:, 1:])

Y = np.random.normal(loc=0.0, scale=1.0, size=10000)
X = np.random.random(size=10000)
lower_right.scatter(X, Y)
top_histogram.hist(X, bins=100)
s = side_histogram.hist(Y, bins=100, orientation='horizontal')

# limpieamos los histogramas  y graficamos los plots normados
top_histogram.clear()
top_histogram.hist(X, bins=100, density=True)
side_histogram.clear()
side_histogram.hist(Y, bins=100, orientation='horizontal', density=True)
# flip the side histogram's x axis
side_histogram.invert_xaxis()

3.6. Boxplots

import pandas as pd
normal_sample = np.random.normal(loc=0.0, scale=1.0, size=10000)
random_sample = np.random.random(size=10000)
gamma_sample = np.random.gamma(2, size=10000)

df = pd.DataFrame({'normal': normal_sample, 
                   'random': random_sample, 
                   'gamma': gamma_sample})

df.describe()

	normal	random	gamma
count	10000.000000	10000.000000	10000.000000
mean	0.022058	0.496203	2.001121
std	1.006828	0.289074	1.421475
min	-3.705981	0.000023	0.007623
25%	-0.666002	0.246149	0.955794
50%	0.015400	0.494168	1.692489
75%	0.708854	0.745258	2.682168
max	3.691711	0.999688	13.809579

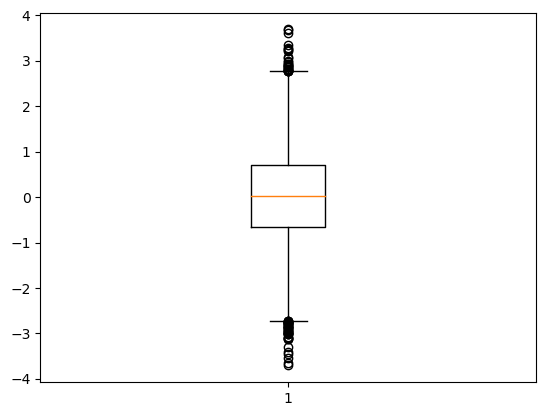
plt.figure()
# crear un diagrama de caja de los datos normales, note el ";" al final
plt.boxplot(df['normal']);

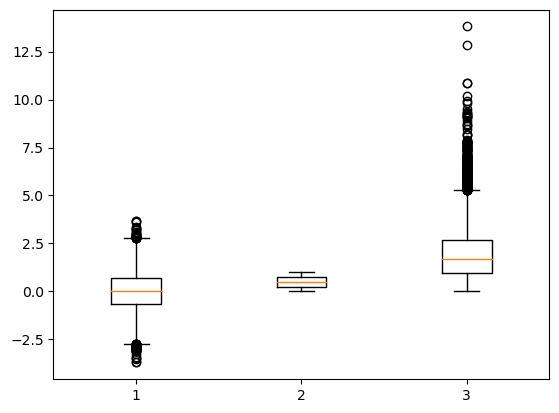
# limpiamos la figura
plt.clf()
# graficamos diagramas de caja para las tres columnas de df
plt.boxplot([ df['normal'], df['random'], df['gamma'] ]);

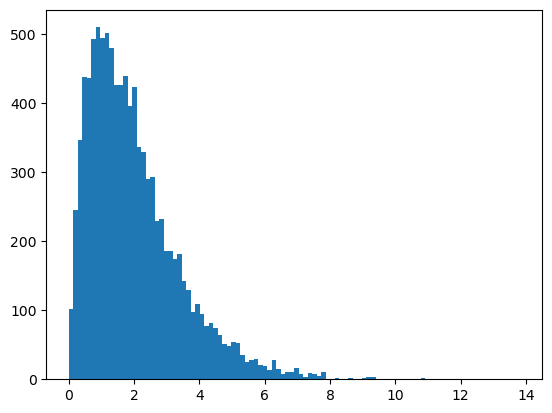
plt.figure()
plt.hist(df['gamma'], bins=100);

import mpl_toolkits.axes_grid1.inset_locator as mpl_il

plt.figure()
plt.boxplot([ df['normal'], df['random'], df['gamma'] ])
# superponer el eje encima de otro
ax2 = mpl_il.inset_axes(plt.gca(), width='60%', height='40%', loc=2)
ax2.hist(df['gamma'], bins=100)
ax2.margins(x=0.5)

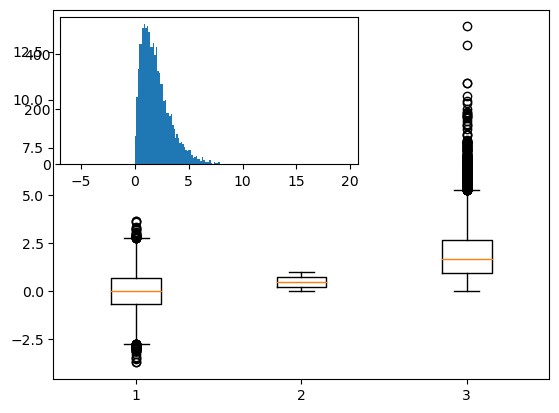
# cambiar las marcas del eje y para ax2 al lado derecho
ax2.yaxis.tick_right()

# si no se pasa el argumento `whis`, el boxplot tiene por default to mostrar 1.5*interquartile (IQR) con outliers
plt.figure()
plt.boxplot([ df['normal'], df['random'], df['gamma'] ] );

3.7. Heatmaps

plt.figure()

Y = np.random.normal(loc=0.0, scale=1.0, size=10000)
X = np.random.random(size=10000)
plt.hist2d(X, Y, bins=25);

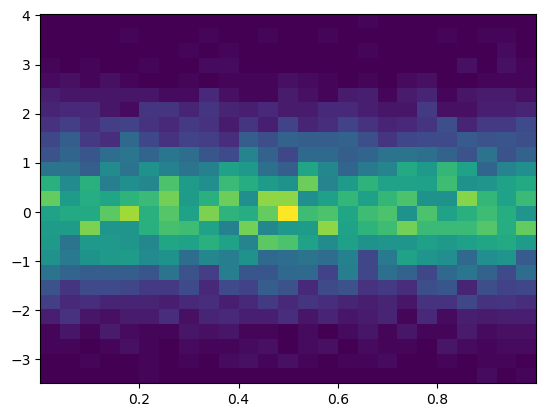
plt.figure()
plt.hist2d(X, Y, bins=100);

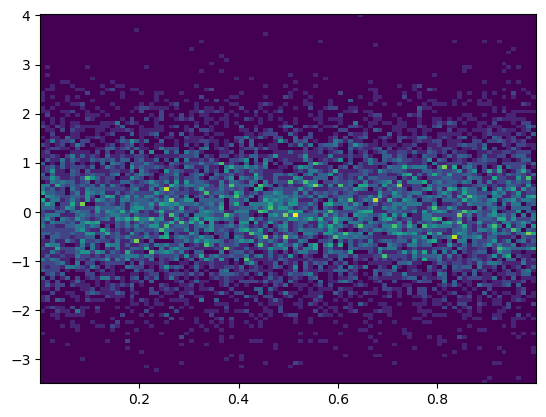
# añadimos la leyenda de colores
plt.colorbar()

---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
Cell In[56], line 2
      1 # añadimos la leyenda de colores
----> 2 plt.colorbar()

File ~/opt/anaconda3/lib/python3.9/site-packages/matplotlib/pyplot.py:2133, in colorbar(mappable, cax, ax, **kwargs)
   2131     mappable = gci()
   2132     if mappable is None:
-> 2133         raise RuntimeError('No mappable was found to use for colorbar '
   2134                            'creation. First define a mappable such as '
   2135                            'an image (with imshow) or a contour set ('
   2136                            'with contourf).')
   2137 ret = gcf().colorbar(mappable, cax=cax, ax=ax, **kwargs)
   2138 return ret

RuntimeError: No mappable was found to use for colorbar creation. First define a mappable such as an image (with imshow) or a contour set (with contourf).

<Figure size 640x480 with 0 Axes>

3.8. Visualización con Pandas

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# consulte los estilos predefinidos proporcionados.
plt.style.available

['Solarize_Light2',
 '_classic_test_patch',
 '_mpl-gallery',
 '_mpl-gallery-nogrid',
 'bmh',
 'classic',
 'dark_background',
 'fast',
 'fivethirtyeight',
 'ggplot',
 'grayscale',
 'seaborn',
 'seaborn-bright',
 'seaborn-colorblind',
 'seaborn-dark',
 'seaborn-dark-palette',
 'seaborn-darkgrid',
 'seaborn-deep',
 'seaborn-muted',
 'seaborn-notebook',
 'seaborn-paper',
 'seaborn-pastel',
 'seaborn-poster',
 'seaborn-talk',
 'seaborn-ticks',
 'seaborn-white',
 'seaborn-whitegrid',
 'tableau-colorblind10']

# usamos el estilo 'seaborn-colorblind'
plt.style.use('seaborn-colorblind')

3.8.1. DataFrame.plot

np.random.seed(123)

df = pd.DataFrame({'A': np.random.randn(365).cumsum(0), 
                   'B': np.random.randn(365).cumsum(0) + 20,
                   'C': np.random.randn(365).cumsum(0) - 20}, 
                  index=pd.date_range('1/1/2017', periods=365))
df.head()

	A	B	C
2017-01-01	-1.085631	20.059291	-20.230904
2017-01-02	-0.088285	21.803332	-16.659325
2017-01-03	0.194693	20.835588	-17.055481
2017-01-04	-1.311601	21.255156	-17.093802
2017-01-05	-1.890202	21.462083	-19.518638

Podemos seleccionar qué gráfico queremos usar pasándolo al parámetro ‘kind’.

df.plot('A','B', kind = 'scatter');

También puede elegir el tipo de figura utilizando los métodos DataFrame.plot.kind en lugar de proporcionar el argumento kind.

kind :

• 'line' : line plot (default)

• 'bar' : vertical bar plot

• 'barh' : horizontal bar plot

• 'hist' : histogram

• 'box' : boxplot

• 'kde' : Kernel Density Estimation plot

• 'density' : same as ‘kde’

• 'area' : area plot

• 'pie' : pie plot

• 'scatter' : scatter plot

• 'hexbin' : hexbin plot

# crear un diagrama de dispersión de las columnas 'A' y 'C', cambiando el color (c) y el tamaño (s) según la columna 'B'
df.plot.scatter('A', 'C', c='B', s=df['B'], colormap='viridis');

ax = df.plot.scatter('A', 'C', c='B', s=df['B'], colormap='viridis')
ax.set_aspect('equal')

df.plot.box();

df.plot.hist(alpha=0.7);

Los gráficos de estimación de densidad con kernel son útiles para derivar una función continua suave a partir de una muestra determinada.

df.plot.kde();

3.8.2. pandas.tools.plotting

#import os as os
#os.chdir("C:/Users/VICTOR/Documents/AnalyticsPython/Data")
iris = pd.read_csv('Data/iris.csv')
iris.head()

	SepalLength	SepalWidth	PetalLength	PetalWidth	Name
0	5.1	3.5	1.4	0.2	Iris-setosa
1	4.9	3.0	1.4	0.2	Iris-setosa
2	4.7	3.2	1.3	0.2	Iris-setosa
3	4.6	3.1	1.5	0.2	Iris-setosa
4	5.0	3.6	1.4	0.2	Iris-setosa

pd.plotting.scatter_matrix(iris);

plt.figure()
#pd.tools.plotting.parallel_coordinates(iris, 'Name');
pd.plotting.parallel_coordinates(iris, 'Name');

3.9. Seaborn

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

np.random.seed(1234)

v1 = pd.Series(np.random.normal(0,10,1000), name='v1')
v2 = pd.Series(2*v1 + np.random.normal(60,15,1000), name='v2')

plt.figure()
plt.hist(v1, alpha=0.7, bins=np.arange(-50,150,5), label='v1');
plt.hist(v2, alpha=0.7, bins=np.arange(-50,150,5), label='v2');
plt.legend();

# graficar la estimación de la densidad del kernel sobre un gráfico de barras apilado
plt.figure()
plt.hist([v1, v2], histtype='barstacked', density=True);
v3 = np.concatenate((v1,v2))
sns.kdeplot(v3);
v3.shape

(2000,)

plt.figure()
# podemos pasar argumentos  para cada componente individual del gráfico
df_aux = pd.DataFrame({'V3':v3})
sns.displot(df_aux,kde = True,stat = 'density')

<seaborn.axisgrid.FacetGrid at 0x7fc721c59820>

sns.jointplot(x=v1,y=v2, alpha=0.4);

grid = sns.jointplot(x=v1,y=v2, alpha=0.4);
grid.ax_joint.set_aspect('equal')

sns.jointplot(x=v1,y=v2, kind='hex');

# establecer el estilo seaborn para todas las siguientes figuras
sns.set_style('white')

sns.jointplot(x=v1,y=v2, kind='kde', space=0);

iris = pd.read_csv('Data/iris.csv')
iris.head()

	SepalLength	SepalWidth	PetalLength	PetalWidth	Name
0	5.1	3.5	1.4	0.2	Iris-setosa
1	4.9	3.0	1.4	0.2	Iris-setosa
2	4.7	3.2	1.3	0.2	Iris-setosa
3	4.6	3.1	1.5	0.2	Iris-setosa
4	5.0	3.6	1.4	0.2	Iris-setosa

sns.pairplot(iris, hue='Name', diag_kind='kde', height=2);

plt.figure(figsize=(8,6))
plt.subplot(121)
kk = 4
sns.swarmplot(x='Name', y='PetalLength', data=iris,s = kk);
plt.subplot(122)
sns.violinplot(x='Name', y='PetalLength', data=iris,s = kk);

3.10. Tips

3.10.1. Creando gráficos

Figure

Operador	Descripción
fig = plt.figures()	un contenedor que contiene todos los elementos del gráfico

Axes

Operador	Descripción
fig.add_axes()	Inicia un subplot
a = fig.add_subplot(222)	Un subplot es un AXES en un grid que tiene sistema fila-columna
fig, b = plt.subplots(nrows=3, nclos=2)	Agrega un subplot
ax = plt.subplots(2, 2)	Crea el subplot

3.10.2. Graficando

Datos 1D

Operador	Descripción
lines = plt.plot(x,y)	Grafica datos conectados por líneas
plt.scatter(x,y)	Crea un gráfico de dispersión
plt.bar(xvalue, data , width, color…)	Gráfico de barras simple vertical
plt.barh(yvalue, data, width, color…)	Gráfico de barras simple horizontal
plt.hist(x, y)	Grafica un hisrograma
plt.boxplot(x,y)	Gráfico de caja y bigotes
plt.violinplot(x, y)	Gráfico de violín
ax.fill(x, y, color=’lightblue’)	Llena el área debajo de la curva
ax.fill_between(x,y,color=’yellow’)	Llena el área entre de la curva

Datos 2D

Operador	Descripción
fig, ax = plt.subplots()
im = ax.imshow(img, cmap, vmin…)	Mapa de colores con arrays RGB

Guardando gráficos

Operador	Descripción
plt.savefig(‘pic.png’)	Se guarda el gráfico
plt.savefig(‘transparentback.png’)	Se guarda el gráfico con fondo transparente

3.10.3. Personalización

Color

Operador	Descripción
plt.plot(x, y, color=’lightblue’)
plt.plot(x, y, alpha = 0.4)	Se fija un color
plt.colorbar(mappable,
orientation=’horizontal’)	mappable: la Image, Contourset etc a los que aplica la barra de colores

Markers

Operador	Descripción
plt.plot(x, y, marker=’o’)	Se agrega el tipo de punto
plt.scatter(x, y, marker=’.’)	Se agrega un ‘.’ en cada punto

Líneas

Operador	Descripción
plt.plot(x, y, linewidth=2)	Se fija el ancho de la línea
plt.plot(x, y, ls=’solid’)	Se fija el estilo de la línea
plt.plot(x, y, ls=’–‘)	Se fija el estilo de la línea
plt.plot(x,y,'--', x**2, y**2, '-.')	Las lineas son '--' y '_.'
plt.setp(lines,color=’red’,linewidth=2)	Fija las propiedades de las lineas

Texto

Operador	Descripción
plt.text(1, 1,’Example
Text’,style=’italic’)	Ubica el texto en las coordenadas 1/1
ax.annotate(‘some annotation’, xy=(10, 10))	Ubica el texto s con coordenadas xy
plt.title(r'$delta_i=20$', fontsize=10)	Expresiones matemáticas

Límites

Operador	Descripción
plt.xlim(0, 7)	Fija el eje-x para mostrar 0-7
other = array.copy()	Crea una copia del array
plt.ylim(-0.5, 9)	Fija el eje-y para mostrar -0.5-9
ax.set(xlim=[0, 7], ylim=[-0.5, 9])
ax.set_xlim(0, 7)	Fija los límites
plt.margins(x=1.0, y=1.0)	Fija los márgenes
plt.axis(‘equal’)	Fija el ratio del gráfico a 1

Leyendas/etiquetas

Operador	Descripción
plt.title(‘just a title’)	Fija el título del gráfico
plt.xlabel(‘x-axis’)	Fija la etiqueta del eje x
plt.ylabel(‘y-axis’)	Fija la etiqueta del eje y
ax.set(title=’axis’, ylabel=’Y-Axis’, xlabel=’X-Axis’)	Fija el título y las etiquetas de los ejes
ax.legend(loc=’best’)	No traslapa los elementos del gráfico

Ticks

Operador	Descripción
plt.xticks(x, labels, rotation=’vertical’)	Fija los ticks
ax.xaxis.set(ticks=range(1,5), ticklabels=[3,100,-12,”foo”])	Fija los ticks de x
ax.tick_params(axis=’y’, direction=’inout’, length=10)	Hace que los ticks sean más largos dentro y fuera