7. Aprendizaje Supervisado

7.1. KNN

Método de los vecinos más cercanos es un método de aprendizaje supervisado.

Importamos las librerías necesarias y los datos

#%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split

uu = 'https://raw.githubusercontent.com/vmoprojs/DataLectures/refs/heads/master/fruit_data_with_colors.txt'
fruits = pd.read_table(uu)

fruits.head()

	fruit_label	fruit_name	fruit_subtype	mass	width	height	color_score
0	1	apple	granny_smith	192	8.4	7.3	0.55
1	1	apple	granny_smith	180	8.0	6.8	0.59
2	1	apple	granny_smith	176	7.4	7.2	0.60
3	2	mandarin	mandarin	86	6.2	4.7	0.80
4	2	mandarin	mandarin	84	6.0	4.6	0.79

# creamos una correspondencia entre la etiqueta y el nombre de la fruta por facilidad de lectura
lookup_fruit_name = dict(zip(fruits.fruit_label.unique(), fruits.fruit_name.unique()))   
lookup_fruit_name

{1: 'apple', 2: 'mandarin', 3: 'orange', 4: 'lemon'}

El archivo contiene la masa, la altura y el ancho de una selección de naranjas, limones y manzanas. Las alturas se midieron a lo largo del corazón de la fruta.

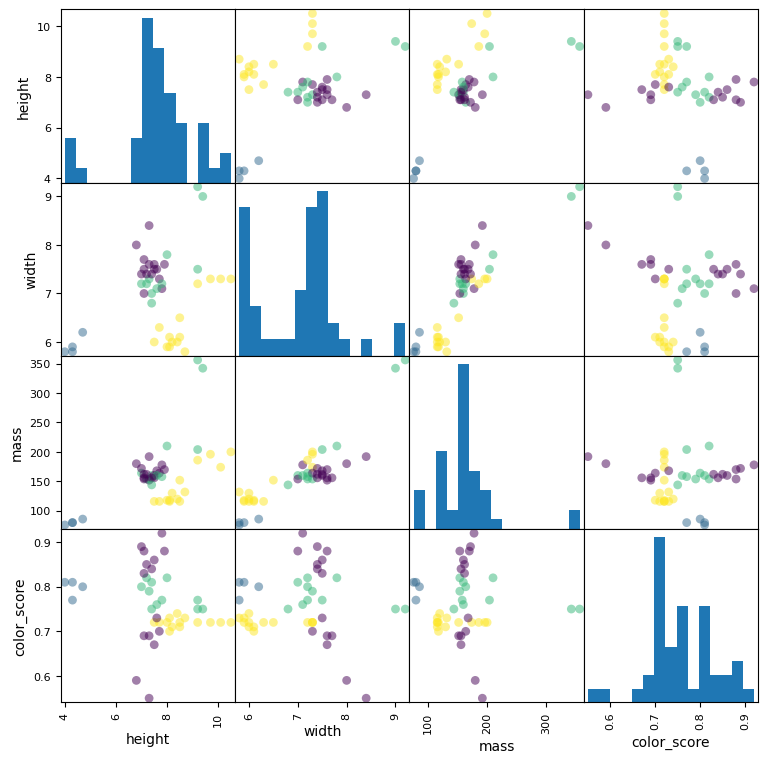
7.1.1. Revisando los datos

# grafico de una matriz scatter
from matplotlib import cm

X = fruits[['height', 'width', 'mass', 'color_score']]
y = fruits['fruit_label']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

scatter = pd.plotting.scatter_matrix(X_train, c= y_train, marker = 'o', s=40, hist_kwds={'bins':15}, figsize=(9,9))

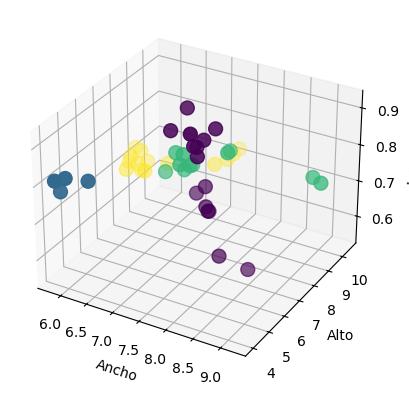
# grafico de 3D scatter plot
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
ax.scatter(X_train['width'], X_train['height'], X_train['color_score'], c = y_train, marker = 'o', s=100)
ax.set_xlabel('Ancho')
ax.set_ylabel('Alto')
ax.set_zlabel('color_score')
plt.show()

7.1.2. Creamos los conjuntos de entrenamiento y prueba

# Para este ejemplo, usamos las características de masa, ancho y alto de cada instancia de fruta.
X = fruits[['mass', 'width', 'height']]
y = fruits['fruit_label']

# default es 75% / 25% train-test split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

7.1.3. Creamos el objeto clasificador

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier(n_neighbors = 5)

7.1.4. Entrenamos el clasificador (ajustamos el modelo) en los datos de entrenamiento

knn.fit(X_train, y_train)

KNeighborsClassifier()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

7.1.5. Estimamos la precisión del clasificador usando los datos de prueba

knn.score(X_test,y_test)

0.5333333333333333

7.1.6. Usar el clasificador para predecir datos no observados

# primer ejemplo: una fruta pequeña con una masa de 20 g, ancho 4,3 cm, altura 5,5 cm
fruit_prediction = knn.predict([[20,4.3,5.5]])
print(fruit_prediction)
lookup_fruit_name[fruit_prediction[0]]

[2]

/Users/victormorales/opt/anaconda3/lib/python3.9/site-packages/sklearn/base.py:464: UserWarning: X does not have valid feature names, but KNeighborsClassifier was fitted with feature names
  warnings.warn(

'mandarin'

7.1.7. Graficamos las fronteras de decisión de KNN

from shared_utilities import plot_fruit_knn

plot_fruit_knn(X_train, y_train, 5, 'uniform')   # elegimos 5 vecinos mas cercanos

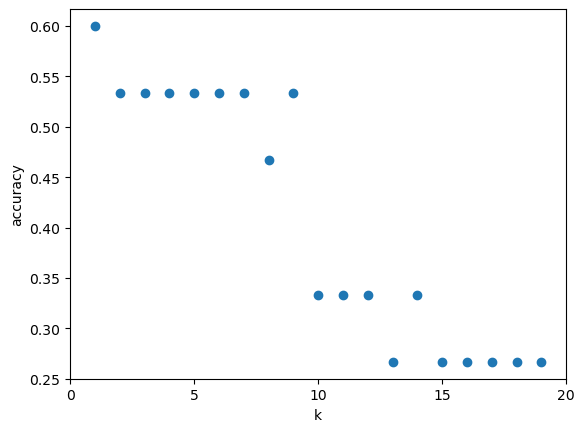
7.1.8. ¿Cuán sensible es la precisión de la clasificación K-NN a la elección de K?

k_range = range(1,20)
scores = []

for k in k_range:
    knn = KNeighborsClassifier(n_neighbors = k)
    knn.fit(X_train, y_train)
    scores.append(knn.score(X_test, y_test))

plt.figure()
plt.xlabel('k')
plt.ylabel('accuracy')
plt.scatter(k_range, scores)
plt.xticks([0,5,10,15,20]); 

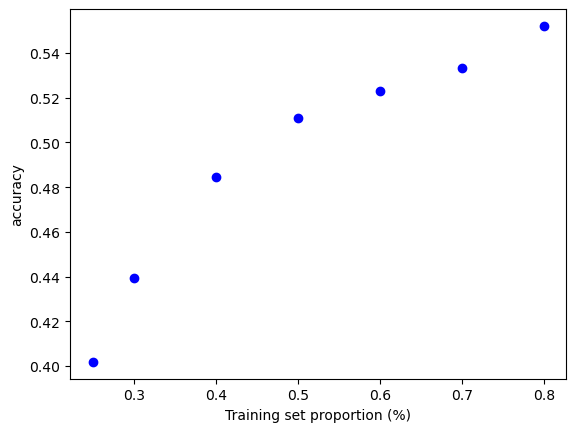
7.1.9. ¿Cuán sensible es la precisión de la clasificación K-NN a la elección de la proporción de la partición?

t = [0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.25]

knn = KNeighborsClassifier(n_neighbors = 5)

plt.figure()

for s in t:

    scores = []
    for i in range(1,1000):
        X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 1-s)
        knn.fit(X_train, y_train)
        scores.append(knn.score(X_test, y_test))
    plt.plot(s, np.mean(scores), 'bo')

plt.xlabel('Training set proportion (%)')
plt.ylabel('accuracy');

7.2. Modelos lineales para regresión

7.2.1. Regresión lineal

# creamos un conjunto de datos para regresion
from sklearn.datasets import make_regression
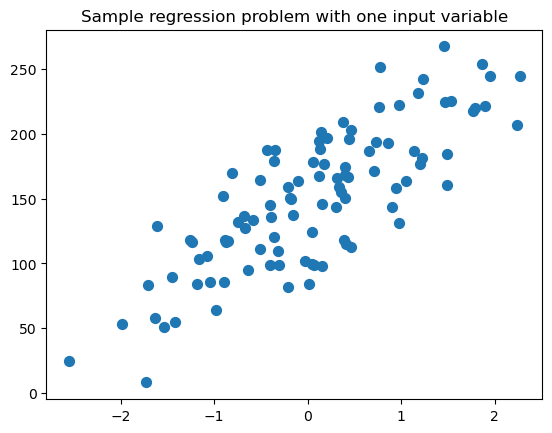
plt.figure()
plt.title('Sample regression problem with one input variable')
X_R1, y_R1 = make_regression(n_samples = 100, n_features=1,
                            n_informative=1, bias = 150.0,
                            noise = 30, random_state=0)
plt.scatter(X_R1, y_R1, marker= 'o', s=50)
plt.show()

from sklearn.linear_model import LinearRegression

X_train, X_test, y_train, y_test = train_test_split(X_R1, y_R1,
                                                   random_state = 0)
linreg = LinearRegression().fit(X_train, y_train)

print('linear model coeff (w): {}'
     .format(linreg.coef_))
print('linear model intercept (b): {:.3f}'
     .format(linreg.intercept_))
print('R-squared score (training): {:.3f}'
     .format(linreg.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'
     .format(linreg.score(X_test, y_test)))

linear model coeff (w): [45.70870465]
linear model intercept (b): 148.446
R-squared score (training): 0.679
R-squared score (test): 0.492

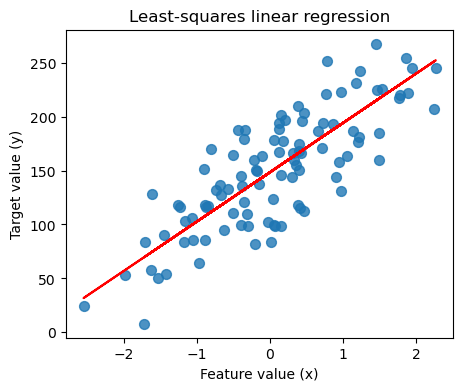
7.2.2. Regresion lineal: un gráfico

plt.figure(figsize=(5,4))
plt.scatter(X_R1, y_R1, marker= 'o', s=50, alpha=0.8)
plt.plot(X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-')
plt.title('Least-squares linear regression')
plt.xlabel('Feature value (x)')
plt.ylabel('Target value (y)')
plt.show()

Si tienes problemas con la instalación de graphviz, visita https://pygraphviz.github.io/documentation/stable/install.html

from shared_utilities import load_crime_dataset
# Comunidades y dataset de crimen
(X_crime, y_crime) = load_crime_dataset()

X_train, X_test, y_train, y_test = train_test_split(X_crime, y_crime,
                                                   random_state = 0)
linreg = LinearRegression().fit(X_train, y_train)

print('Crime dataset')
print('linear model intercept: {}'
     .format(linreg.intercept_))
print('linear model coeff:\n{}'
     .format(linreg.coef_))
print('R-squared score (training): {:.3f}'
     .format(linreg.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'
     .format(linreg.score(X_test, y_test)))

Crime dataset
linear model intercept: -1728.1306725953114
linear model coeff:
[ 1.61892346e-03 -9.43009110e+01  1.36067510e+01 -3.13380670e+01
 -8.15482723e-02 -1.69455128e+01 -2.42730375e-03  1.53013232e+00
 -1.39193248e-02 -7.72112833e+00  2.28112354e+01 -5.65708295e+00
  9.34751364e+00  2.06969566e-01 -7.43413626e+00  9.65856476e-03
  4.38030290e-03  4.79754625e-03 -4.46469212e+00 -1.60907140e+01
  8.82778012e+00 -5.06734503e-01 -1.42198055e+00  8.17551991e+00
 -3.87048268e+00 -3.54209213e+00  4.48758304e+00  9.30645715e+00
  1.73644996e+02  1.18220766e+01  1.51120836e+02 -3.29613007e+02
 -1.35343395e+02  6.95380108e-01 -2.38369008e+01  2.77038981e+00
  3.82248925e-01  4.38813358e+00 -1.06410851e+01 -4.92294176e-03
  4.14031827e+01 -1.16206866e-03  1.18568968e+00  1.75418465e+00
 -3.68283678e+00  1.59679443e+00 -8.42180230e+00 -3.79703897e+01
  4.74076990e+01 -2.50768374e+01 -2.88246410e-01 -3.65633234e+01
  1.89516080e+01 -4.53336736e+01  6.82698598e+02  1.04478671e+02
 -3.28575414e+02 -3.14364068e+01  2.74053494e+01  5.12336432e+00
  6.91580764e+01  1.98267157e-02 -6.12133638e-01  2.65335065e+01
  1.00704633e+01 -1.58621594e+00  2.24025322e+00  7.38288450e+00
 -3.13915504e+01 -9.78026040e-05  5.01970944e-05 -3.48042555e-04
 -2.50242794e-04 -5.26610456e-01 -5.16564774e-01 -4.10464090e-01
  1.16146366e-01  1.46167357e+00 -3.04019816e-01  2.43792841e+00
 -3.65615457e+01  1.41488917e-01  2.88800603e-01  1.77464865e+01
  5.96587698e-01  1.98257510e+00 -1.36380442e-01 -1.85303461e+00]
R-squared score (training): 0.673
R-squared score (test): 0.496

7.2.3. Regresión Ridge

from sklearn.linear_model import Ridge
X_train, X_test, y_train, y_test = train_test_split(X_crime, y_crime,
                                                   random_state = 0)

linridge = Ridge(alpha=20.0).fit(X_train, y_train)

print('Crime dataset')
print('ridge regression linear model intercept: {}'
     .format(linridge.intercept_))
print('ridge regression linear model coeff:\n{}'
     .format(linridge.coef_))
print('R-squared score (training): {:.3f}'
     .format(linridge.score(X_train, y_train)))
print('R-squared score (test): {:.3f}'
     .format(linridge.score(X_test, y_test)))
print('Number of non-zero features: {}'
     .format(np.sum(linridge.coef_ != 0)))

Crime dataset
ridge regression linear model intercept: -3352.4230358461637
ridge regression linear model coeff:
[ 1.95091438e-03  2.19322667e+01  9.56286607e+00 -3.59178973e+01
  6.36465325e+00 -1.96885471e+01 -2.80715856e-03  1.66254486e+00
 -6.61426604e-03 -6.95450680e+00  1.71944731e+01 -5.62819154e+00
  8.83525114e+00  6.79085746e-01 -7.33614221e+00  6.70389803e-03
  9.78505502e-04  5.01202169e-03 -4.89870524e+00 -1.79270062e+01
  9.17572382e+00 -1.24454193e+00  1.21845360e+00  1.03233089e+01
 -3.78037278e+00 -3.73428973e+00  4.74595305e+00  8.42696855e+00
  3.09250005e+01  1.18644167e+01 -2.05183675e+00 -3.82210450e+01
  1.85081589e+01  1.52510829e+00 -2.20086608e+01  2.46283912e+00
  3.29328703e-01  4.02228467e+00 -1.12903533e+01 -4.69567413e-03
  4.27046505e+01 -1.22507167e-03  1.40795790e+00  9.35041855e-01
 -3.00464253e+00  1.12390514e+00 -1.82487653e+01 -1.54653407e+01
  2.41917002e+01 -1.32497562e+01 -4.20113118e-01 -3.59710660e+01
  1.29786751e+01 -2.80765995e+01  4.38513476e+01  3.86590044e+01
 -6.46024046e+01 -1.63714023e+01  2.90397330e+01  4.15472907e+00
  5.34033563e+01  1.98773191e-02 -5.47413979e-01  1.23883518e+01
  1.03526583e+01 -1.57238894e+00  3.15887097e+00  8.77757987e+00
 -2.94724962e+01 -2.32601756e-04  3.13528914e-04 -4.14022055e-04
 -1.79457415e-04 -5.74054527e-01 -5.17742507e-01 -4.20670931e-01
  1.53383594e-01  1.32725423e+00  3.84863158e+00  3.03024594e+00
 -3.77692644e+01  1.37933464e-01  3.07676522e-01  1.57128807e+01
  3.31418306e-01  3.35994414e+00  1.61265911e-01 -2.67619878e+00]
R-squared score (training): 0.671
R-squared score (test): 0.494
Number of non-zero features: 88

7.2.3.1. Regresión Ridge con variables normalizadas

from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()

from sklearn.linear_model import Ridge
X_train, X_test, y_train, y_test = train_test_split(X_crime, y_crime,
                                                   random_state = 0)

X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

linridge = Ridge(alpha=20.0).fit(X_train_scaled, y_train)

print('Crime dataset')
print('ridge regression linear model intercept: {}'
     .format(linridge.intercept_))
print('ridge regression linear model coeff:\n{}'
     .format(linridge.coef_))
print('R-squared score (training): {:.3f}'
     .format(linridge.score(X_train_scaled, y_train)))
print('R-squared score (test): {:.3f}'
     .format(linridge.score(X_test_scaled, y_test)))
print('Number of non-zero features: {}'
     .format(np.sum(linridge.coef_ != 0)))

Crime dataset
ridge regression linear model intercept: 933.3906385044168
ridge regression linear model coeff:
[  88.68827454   16.48947987  -50.30285445  -82.90507574  -65.89507244
   -2.27674244   87.74108514  150.94862182   18.8802613   -31.05554992
  -43.13536109 -189.44266328   -4.52658099  107.97866804  -76.53358414
    2.86032762   34.95230077   90.13523036   52.46428263  -62.10898424
  115.01780357    2.66942023    6.94331369   -5.66646499 -101.55269144
  -36.9087526    -8.7053343    29.11999068  171.25963057   99.36919476
   75.06611841  123.63522539   95.24316483 -330.61044265 -442.30179004
 -284.49744001 -258.37150609   17.66431072 -101.70717151  110.64762887
  523.13611718   24.8208959     4.86533322  -30.46775619   -3.51753937
   50.57947231   10.84840601   18.27680946   44.11189865   58.33588176
   67.08698975  -57.93524659  116.1446052    53.81163718   49.01607711
   -7.62262031   55.14288543  -52.08878272  123.39291017   77.12562171
   45.49795317  184.91229771  -91.35721203    1.07975971  234.09267451
   10.3887921    94.7171829   167.91856631  -25.14025088   -1.18242839
   14.60362467   36.77122659   53.19878339  -78.86365997   -5.89858411
   26.04790298  115.1534917    68.74143311   68.28588166   16.5260514
  -97.90513652  205.20448474   75.97304123   61.3791085   -79.83157049
   67.26700741   95.67094538  -11.88380569]
R-squared score (training): 0.615
R-squared score (test): 0.599
Number of non-zero features: 88

7.2.3.2. Regresión Ridge con parámetro de regularización alpha

print('Ridge regression: effect of alpha regularization parameter\n')
for this_alpha in [0, 1, 10, 20, 50, 100, 1000]:
    linridge = Ridge(alpha = this_alpha).fit(X_train_scaled, y_train)
    r2_train = linridge.score(X_train_scaled, y_train)
    r2_test = linridge.score(X_test_scaled, y_test)
    num_coeff_bigger = np.sum(abs(linridge.coef_) > 1.0)
    print('Alpha = {:.2f}\nnum abs(coeff) > 1.0: {}, \
r-squared training: {:.2f}, r-squared test: {:.2f}\n'
         .format(this_alpha, num_coeff_bigger, r2_train, r2_test))

Ridge regression: effect of alpha regularization parameter

Alpha = 0.00
num abs(coeff) > 1.0: 88, r-squared training: 0.67, r-squared test: 0.49

Alpha = 1.00
num abs(coeff) > 1.0: 87, r-squared training: 0.66, r-squared test: 0.56

Alpha = 10.00
num abs(coeff) > 1.0: 87, r-squared training: 0.63, r-squared test: 0.59

Alpha = 20.00
num abs(coeff) > 1.0: 88, r-squared training: 0.61, r-squared test: 0.60

Alpha = 50.00
num abs(coeff) > 1.0: 86, r-squared training: 0.58, r-squared test: 0.58

Alpha = 100.00
num abs(coeff) > 1.0: 87, r-squared training: 0.55, r-squared test: 0.55

Alpha = 1000.00
num abs(coeff) > 1.0: 84, r-squared training: 0.31, r-squared test: 0.30

7.2.4. Regresión Lasso

from sklearn.linear_model import Lasso
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()

X_train, X_test, y_train, y_test = train_test_split(X_crime, y_crime,
                                                   random_state = 0)

X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

linlasso = Lasso(alpha=2.0, max_iter = 10000).fit(X_train_scaled, y_train)

print('Crime dataset')
print('lasso regression linear model intercept: {}'
     .format(linlasso.intercept_))
print('lasso regression linear model coeff:\n{}'
     .format(linlasso.coef_))
print('Non-zero features: {}'
     .format(np.sum(linlasso.coef_ != 0)))
print('R-squared score (training): {:.3f}'
     .format(linlasso.score(X_train_scaled, y_train)))
print('R-squared score (test): {:.3f}\n'
     .format(linlasso.score(X_test_scaled, y_test)))
print('Features with non-zero weight (sorted by absolute magnitude):')

for e in sorted (list(zip(list(X_crime), linlasso.coef_)),
                key = lambda e: -abs(e[1])):
    if e[1] != 0:
        print('\t{}, {:.3f}'.format(e[0], e[1]))

Crime dataset
lasso regression linear model intercept: 1186.612061998579
lasso regression linear model coeff:
[    0.             0.            -0.          -168.18346054
    -0.            -0.             0.           119.6938194
     0.            -0.             0.          -169.67564456
    -0.             0.            -0.             0.
     0.             0.            -0.            -0.
     0.            -0.             0.             0.
   -57.52991966    -0.            -0.             0.
   259.32889226    -0.             0.             0.
     0.            -0.         -1188.7396867     -0.
    -0.            -0.          -231.42347299     0.
  1488.36512229     0.            -0.            -0.
    -0.             0.             0.             0.
     0.             0.            -0.             0.
    20.14419415     0.             0.             0.
     0.             0.           339.04468804     0.
     0.           459.53799903    -0.             0.
   122.69221826    -0.            91.41202242     0.
    -0.             0.             0.            73.14365856
     0.            -0.             0.             0.
    86.35600042     0.             0.             0.
  -104.57143405   264.93206555     0.            23.4488645
   -49.39355188     0.             5.19775369     0.        ]
Non-zero features: 20
R-squared score (training): 0.631
R-squared score (test): 0.624

Features with non-zero weight (sorted by absolute magnitude):
	PctKidsBornNeverMar, 1488.365
	PctKids2Par, -1188.740
	HousVacant, 459.538
	PctPersDenseHous, 339.045
	NumInShelters, 264.932
	MalePctDivorce, 259.329
	PctWorkMom, -231.423
	pctWInvInc, -169.676
	agePct12t29, -168.183
	PctVacantBoarded, 122.692
	pctUrban, 119.694
	MedOwnCostPctIncNoMtg, -104.571
	MedYrHousBuilt, 91.412
	RentQrange, 86.356
	OwnOccHiQuart, 73.144
	PctEmplManu, -57.530
	PctBornSameState, -49.394
	PctForeignBorn, 23.449
	PctLargHouseFam, 20.144
	PctSameCity85, 5.198

7.2.4.1. Regresión Lasso con parámetro de regularización alpha

print('Lasso regression: effect of alpha regularization\n\
parameter on number of features kept in final model\n')

for alpha in [0.5, 1, 2, 3, 5, 10, 20, 50]:
    linlasso = Lasso(alpha, max_iter = 10000).fit(X_train_scaled, y_train)
    r2_train = linlasso.score(X_train_scaled, y_train)
    r2_test = linlasso.score(X_test_scaled, y_test)
    
    print('Alpha = {:.2f}\nFeatures kept: {}, r-squared training: {:.2f}, \
r-squared test: {:.2f}\n'
         .format(alpha, np.sum(linlasso.coef_ != 0), r2_train, r2_test))

Lasso regression: effect of alpha regularization
parameter on number of features kept in final model

Alpha = 0.50
Features kept: 35, r-squared training: 0.65, r-squared test: 0.58

Alpha = 1.00
Features kept: 25, r-squared training: 0.64, r-squared test: 0.60

Alpha = 2.00
Features kept: 20, r-squared training: 0.63, r-squared test: 0.62

Alpha = 3.00
Features kept: 17, r-squared training: 0.62, r-squared test: 0.63

Alpha = 5.00
Features kept: 12, r-squared training: 0.60, r-squared test: 0.61

Alpha = 10.00
Features kept: 6, r-squared training: 0.57, r-squared test: 0.58

Alpha = 20.00
Features kept: 2, r-squared training: 0.51, r-squared test: 0.50

Alpha = 50.00
Features kept: 1, r-squared training: 0.31, r-squared test: 0.30

7.3. Árboles de decisión

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from shared_utilities import plot_decision_tree
from sklearn.model_selection import train_test_split


iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state = 3)
clf = DecisionTreeClassifier().fit(X_train, y_train)

print('Accuracy of Decision Tree classifier on training set: {:.2f}'
     .format(clf.score(X_train, y_train)))
print('Accuracy of Decision Tree classifier on test set: {:.2f}'
     .format(clf.score(X_test, y_test)))

Accuracy of Decision Tree classifier on training set: 1.00
Accuracy of Decision Tree classifier on test set: 0.95

7.3.1. Establecer la profundidad máxima del árbol de decisión para ayudar a evitar el sobreajuste

clf2 = DecisionTreeClassifier(max_depth = 3).fit(X_train, y_train)

print('Accuracy of Decision Tree classifier on training set: {:.2f}'
     .format(clf2.score(X_train, y_train)))
print('Accuracy of Decision Tree classifier on test set: {:.2f}'
     .format(clf2.score(X_test, y_test)))

Accuracy of Decision Tree classifier on training set: 0.98
Accuracy of Decision Tree classifier on test set: 0.97

7.3.2. Visualizando árboles de decisión

plot_decision_tree(clf, iris.feature_names, iris.target_names)

7.3.3. Versión Pre-pruned (max_depth = 3)

plot_decision_tree(clf2, iris.feature_names, iris.target_names)

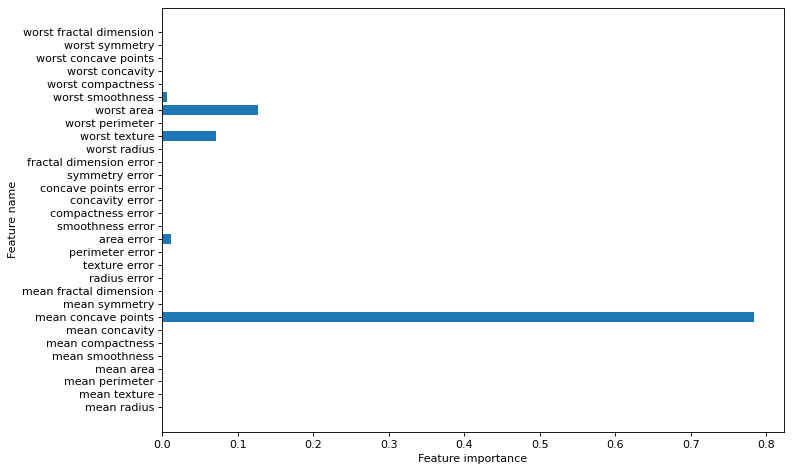
7.3.3.1. Feature importance

from shared_utilities import plot_feature_importances

plt.figure(figsize=(10,4), dpi=80)
plot_feature_importances(clf, iris.feature_names)
plt.show()

print('Feature importances: {}'.format(clf.feature_importances_))

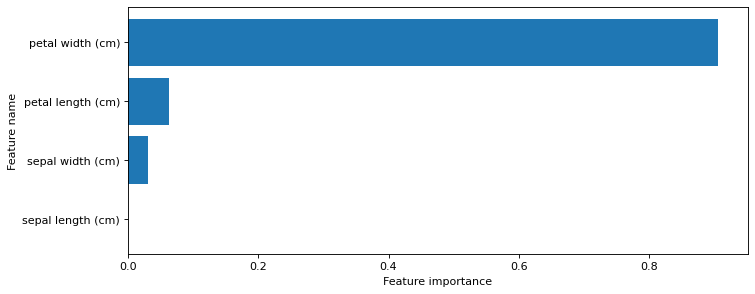
Feature importances: [0.00670338 0.03128242 0.54643762 0.41557658]

from sklearn.tree import DecisionTreeClassifier
from shared_utilities import plot_class_regions_for_classifier_subplot

X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state = 0)
fig, subaxes = plt.subplots(6, 1, figsize=(6, 32))

pair_list = [[0,1], [0,2], [0,3], [1,2], [1,3], [2,3]]
tree_max_depth = 4

for pair, axis in zip(pair_list, subaxes):
    X = X_train[:, pair]
    y = y_train
    
    clf = DecisionTreeClassifier(max_depth=tree_max_depth).fit(X, y)
    title = 'Decision Tree, max_depth = {:d}'.format(tree_max_depth)
    plot_class_regions_for_classifier_subplot(clf, X, y, None,
                                             None, title, axis,
                                             iris.target_names)
    
    axis.set_xlabel(iris.feature_names[pair[0]])
    axis.set_ylabel(iris.feature_names[pair[1]])
    
plt.tight_layout()
plt.show()

7.3.3.2. Ejemplo

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
(X_cancer, y_cancer) = load_breast_cancer(return_X_y = True)


from sklearn.tree import DecisionTreeClassifier
from shared_utilities import plot_decision_tree
from shared_utilities import plot_feature_importances

X_train, X_test, y_train, y_test = train_test_split(X_cancer, y_cancer, random_state = 0)

clf = DecisionTreeClassifier(max_depth = 4, min_samples_leaf = 8,
                            random_state = 0).fit(X_train, y_train)

plot_decision_tree(clf, cancer.feature_names, cancer.target_names)

print('Breast cancer dataset: decision tree')
print('Accuracy of DT classifier on training set: {:.2f}'
     .format(clf.score(X_train, y_train)))
print('Accuracy of DT classifier on test set: {:.2f}'
     .format(clf.score(X_test, y_test)))

plt.figure(figsize=(10,6),dpi=80)
plot_feature_importances(clf, cancer.feature_names)
plt.tight_layout()

plt.show()

Breast cancer dataset: decision tree
Accuracy of DT classifier on training set: 0.96
Accuracy of DT classifier on test set: 0.94