9. Modelos de Probabilidad#
9.1. Probabilidad lineal#
En este caso la variable dependiente es una dummy
Se trata de modelos del tipo:
\[
D_{i} = \beta_{0}+\beta_{1}X_{1i}+u_{i}
\]
Veamos un ejemplo: Abrir la base MROZ de Wooldridge y ajuste el modelo:
\[
inlf=\beta_0nwifeinc+\beta_1educ + \beta_2exper +\beta_3expersq + \beta_4age + \beta_5kidslt6 + \beta_6kidsge6
\]
# Importa la biblioteca pandas para manipulación y análisis de datos
import pandas as pd
# Importa matplotlib para generación de gráficos
import matplotlib.pyplot as plt
# Importa numpy para operaciones numéricas y manejo de arrays
import numpy as np
# Configuración opcional de numpy para mostrar arrays con 2 decimales (comentada)
# np.set_printoptions(precision=2)
# Define la URL del archivo CSV con los datos del estudio Mroz
uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/WO/mroz.csv"
# Carga el archivo CSV desde la URL en un DataFrame de pandas, sin encabezado (header=None)
datos = pd.read_csv(uu, header=None)
# Asigna nombres descriptivos a las columnas del DataFrame
datos.columns = ["inlf", "hours", "kidslt6", "kidsge6",
"age", "educ", "wage",
"repwage", "hushrs", "husage", "huseduc",
"huswage", "faminc", "mtr", "motheduc",
"fatheduc", "unem", "city", "exper",
"nwifeinc", "lwage", "expersq"]
# Importa la API de fórmulas de statsmodels para estimar modelos de regresión
import statsmodels.formula.api as smf
# Importa función para añadir líneas de regresión a gráficos
from statsmodels.graphics.regressionplots import abline_plot
# Importa el módulo de estadística de scipy para funciones estadísticas
from scipy import stats
# Define y ajusta un modelo de regresión lineal usando la fórmula especificada
# La variable dependiente es "inlf" (participación laboral femenina)
# Las variables independientes son ingreso no laboral de la esposa, educación,
# experiencia laboral, su cuadrado, edad, número de hijos menores de 6 y mayores de 6
reg1 = smf.ols('inlf ~ nwifeinc + educ + exper + expersq + age + kidslt6 + kidsge6', data=datos).fit()
print(reg1.summary())
OLS Regression Results
==============================================================================
Dep. Variable: inlf R-squared: 0.264
Model: OLS Adj. R-squared: 0.257
Method: Least Squares F-statistic: 38.22
Date: Wed, 04 Jun 2025 Prob (F-statistic): 6.90e-46
Time: 06:05:26 Log-Likelihood: -423.89
No. Observations: 753 AIC: 863.8
Df Residuals: 745 BIC: 900.8
Df Model: 7
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.5855 0.154 3.798 0.000 0.283 0.888
nwifeinc -0.0034 0.001 -2.351 0.019 -0.006 -0.001
educ 0.0380 0.007 5.151 0.000 0.024 0.052
exper 0.0395 0.006 6.962 0.000 0.028 0.051
expersq -0.0006 0.000 -3.227 0.001 -0.001 -0.000
age -0.0161 0.002 -6.476 0.000 -0.021 -0.011
kidslt6 -0.2618 0.034 -7.814 0.000 -0.328 -0.196
kidsge6 0.0130 0.013 0.986 0.324 -0.013 0.039
==============================================================================
Omnibus: 169.137 Durbin-Watson: 0.494
Prob(Omnibus): 0.000 Jarque-Bera (JB): 36.741
Skew: -0.196 Prob(JB): 1.05e-08
Kurtosis: 1.991 Cond. No. 3.06e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 3.06e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
¿Qué hemos ajustado?
aux = smf.ols('inlf ~ educ',data = datos).fit()
plt.figure()
plt.plot(datos.educ,datos.inlf,'o');
plt.plot(datos.educ,aux.fittedvalues,'-',color='r');
plt.xlabel('educ');
plt.ylabel('inlf');
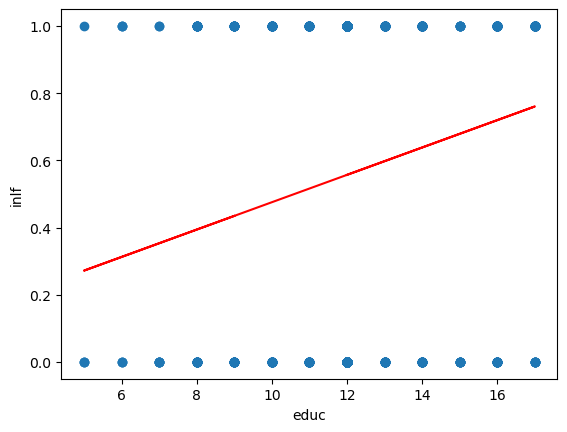
Excepto kidsge6 los coeficientes son significativos.
Se introdujo la experiencia cuadrática para capturar un efecto decreciente en el efecto deseado (
inlf). ¿Cómo lo interpretamos?
.039 - 2(.0006)exper = 0.39 - .0012exper
El punto en el que la experiencia ya no tiene efecto en
inlfes \(.039/.0012 = 32.5\). ¿Cuantos elementos de la muestra tienen más de 32 años de experiencia?
Se añade exper al cuadrado porque queremos dar la posibilidad que los años adicionales de expericnecia contribuyan con un efecto decreciente.
Trabajemos ahora con la predicción, y revisemos el resultado:
pred_vals = reg1.predict()
aux = list(zip(datos.inlf,pred_vals))
print(aux[0:5])
stats.describe(pred_vals)
[(1, 0.6636123221355532), (1, 0.700916572727416), (1, 0.6727286212890488), (1, 0.7257441305286614), (1, 0.5616358247349613)]
DescribeResult(nobs=753, minmax=(-0.34511026465740635, 1.1271505290421107), mean=0.5683930942895071, variance=0.06490433214015512, skewness=-0.42412518180534475, kurtosis=-0.07391834122183871)
¿Qué podemos notar?
Existen valores mayores a 1 e inferiores a 0.
\(R^{2}\) ya no es interpretable en estas regresiones.
Usaremos una probabilidad de ocurrencia, digamos 0.5
prediccion_dum = (pred_vals>=0.5)*1
tab = pd.crosstab(datos.inlf,prediccion_dum)
(tab.iloc[0,0]+tab.iloc[1,1])/datos.shape[0]
0.7343957503320053
9.2. Logit#
La regresión logística puede entenderse simplemente como encontrar los parámtros \(\beta\) que mejor asjuten:
\[\begin{split}
y={\begin{cases}1&\beta_{1}+\beta_{2}X_{1}+\cdots+\beta_{k}X_{k}+u >0\\0&{\text{en otro caso}}\end{cases}}
\end{split}\]
Donde se asume que el error tiene una distribución logística estándar
\[
{\displaystyle f(x;\mu ,s)={\frac {e^{-{\frac {x-\mu }{s}}}}{s\left(1+e^{-{\frac {x-\mu }{s}}}\right)^{2}}}={\frac {1}{s\left(e^{\frac {x-\mu }{2s}}+e^{-{\frac {x-\mu }{2s}}}\right)^{2}}}={\frac {1}{4s}}\operatorname {sech} ^{2}\!\left({\frac {x-\mu }{2s}}\right).}
\]
Donde \(s\) es el parámetro de escala y \(\mu\) el de locación (sech es la función secante hiperbólico).
Otra forma de entender la regresión logística es a través de la función logística:
\[
\sigma (t)={\frac {e^{t}}{e^{t}+1}}={\frac {1}{1+e^{-t}}}
\]
donde \(t\in \mathbb{R}\) y \(0\leq\sigma (t)\leq1\).
Asumiento \(t\) como una función lineal de una variable explicativa \(x\), tenemos:
\[
t=\beta _{0}+\beta _{1}x
\]
Ahora la función logística se puede expresar:
\[
p(x)={\frac {1}{1+e^{-(\beta _{0}+\beta _{1}x)}}}
\]
Ten en cuenta que \(p (x)\) se interpreta como la probabilidad de que la variable dependiente iguale a éxito en lugar de un fracaso. Está claro que las variables de respuesta \(Y_ {i}\) no se distribuyen de forma idéntica: \( P (Y_ {i} = 1 \ mid X )\) difiere de un punto \(X_ {i}\) a otro, aunque son independientes dado que la matriz de diseño \(X\) y los parámetros compartidos \(\beta\).
Finalmente definimos la inversa de la función logística, \(g\), el logit (log odds):
\[
{\displaystyle g(p(x))=\ln \left({\frac {p(x)}{1-p(x)}}\right)=\beta _{0}+\beta _{1}x,}
\]
lo que es equivalente a:
\[
{\frac {p(x)}{1-p(x)}}=e^{\beta _{0}+\beta _{1}x}
\]
Interpretación:
\(g\) es la función logit. La ecuación para \(g (p (x))\) ilustra que el logit (es decir, log-odds o logaritmo natural de las probabilidades) es equivalente a la expresión de regresión lineal.
\(ln\) denota el logaritmo natural.
\(p (x)\) es la probabilidad de que la variable dependiente sea igual a un caso, dada alguna combinación lineal de los predictores. La fórmula para \(p (x)\) ilustra que la probabilidad de que la variable dependiente iguale un caso es igual al valor de la función logística de la expresión de regresión lineal. Esto es importante porque muestra que el valor de la expresión de regresión lineal puede variar de infinito negativo a positivo y, sin embargo, después de la transformación, la expresión resultante para la probabilidad \(p (x)\) oscila entre \(0\) y \(1\).
\(\beta _ {0}\) es la intersección de la ecuación de regresión lineal (el valor del criterio cuando el predictor es igual a cero).
\(\beta _ {1} x\) es el coeficiente de regresión multiplicado por algún valor del predictor.
la base \(e\) denota la función exponencial.
9.2.1. Ejemplo 1#
Abra la tabla 15.7
Los datos son el efecto del Sistema de Enseñanza Personalizada (PSI) sobre las calificaciones.
Calificación \(Y = 1\) si la calificación final fue A
\(Y = 0\) si la calificación final fue B o C
TUCE= calificación en un examen presentado al comienzo del curso para evaluar los conocimientos previos de macroeconomíaPSI= 1 con el nuevo método de enseñanza, 0 en otro casoGPA= promedio de puntos de calificación inicial
Ajuste el siguiente modelo:
smf.logit('GRADE ~ GPA + TUCE + PSI',data = datos).fit()Interprete el modelo
En los modelos cuya variable regresada binaria, la bondad del ajuste tiene una importancia secundaria. Lo que interesa son los signos esperados de los coeficientes de la regresión y su importancia práctica y/o estadística.
Importamos los datos y revisamos la variable dependiente:
uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/tabla15_7.csv"
datos = pd.read_csv(uu,sep = ';')
datos.columns
# import statsmodels.api as sm
datos.pivot_table(index = 'GRADE', aggfunc = [len])
| len | |||||
|---|---|---|---|---|---|
| GPA | LETTER | OBS | PSI | TUCE | |
| GRADE | |||||
| 0 | 21 | 21 | 21 | 21 | 21 |
| 1 | 11 | 11 | 11 | 11 | 11 |
Ajustamos el modelo:
ajuste1 = smf.logit('GRADE ~ GPA + TUCE + PSI',data = datos).fit()
print(ajuste1.summary())
Optimization terminated successfully.
Current function value: 0.402801
Iterations 7
Logit Regression Results
==============================================================================
Dep. Variable: GRADE No. Observations: 32
Model: Logit Df Residuals: 28
Method: MLE Df Model: 3
Date: Wed, 04 Jun 2025 Pseudo R-squ.: 0.3740
Time: 06:05:26 Log-Likelihood: -12.890
converged: True LL-Null: -20.592
Covariance Type: nonrobust LLR p-value: 0.001502
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -13.0213 4.931 -2.641 0.008 -22.687 -3.356
GPA 2.8261 1.263 2.238 0.025 0.351 5.301
TUCE 0.0952 0.142 0.672 0.501 -0.182 0.373
PSI 2.3787 1.065 2.234 0.025 0.292 4.465
==============================================================================
ajuste1.get_margeff(at='mean').summary()
| Dep. Variable: | GRADE |
|---|---|
| Method: | dydx |
| At: | mean |
| dy/dx | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| GPA | 0.5339 | 0.237 | 2.252 | 0.024 | 0.069 | 0.998 |
| TUCE | 0.0180 | 0.026 | 0.685 | 0.493 | -0.033 | 0.069 |
| PSI | 0.4493 | 0.197 | 2.284 | 0.022 | 0.064 | 0.835 |
mm = ajuste1.get_margeff(at='all').margeff
mm[0:10,:]
array([[0.07311607, 0.00246188, 0.06154047],
[0.15815168, 0.0053251 , 0.1331134 ],
[0.43011639, 0.01448239, 0.36202116],
[0.07130492, 0.0024009 , 0.06001605],
[0.69272252, 0.02332457, 0.58305197],
[0.09507939, 0.00320141, 0.08002659],
[0.0729182 , 0.00245522, 0.06137393],
[0.1381988 , 0.00465327, 0.11631942],
[0.2791564 , 0.00939944, 0.23496087],
[0.60069976, 0.02022608, 0.50559808]])
¿Son, en conjunto, los coeficientes significativos?
hyp = '(Intercept = 0, GPA = 0,TUCE=0,PSI=0)'
ajuste1.wald_test(hyp,scalar = True)
<class 'statsmodels.stats.contrast.ContrastResults'>
<Wald test (chi2): statistic=8.873128862019758, p-value=0.06435007959303814, df_denom=4>
np.exp(ajuste1.params)
Intercept 0.000002
GPA 16.879715
TUCE 1.099832
PSI 10.790732
dtype: float64
Esto indica que los estudiantes expuestos al nuevo método de enseñanza son 10 veces más propensos a obtener una A que quienes no están expuestos al nuevo método, en tanto no cambien los demás factores.
ajuste1.predict(which = 'linear')
array([-3.60073413, -2.76041291, -1.46791368, -3.62720615, 0.28141441,
-3.32098459, -3.60359585, -2.91209282, -2.07928416, 0.81658669,
-3.68551751, -1.45002683, -0.74349868, -1.42927827, -0.5710702 ,
-3.46980278, -2.87059569, -3.21545265, 0.3634383 , 0.66679813,
-2.72739871, 2.25228291, -1.14298655, 1.7510952 , 1.64556325,
-0.0755037 , 0.55554274, -0.8131547 , 1.67096266, 2.85041739,
0.11660073, -2.08025454])
9.2.2. Ejemplo 2#
Este ejemplo tiene por objetivo lograr la mejor predicción de actividades ilícitas (Uafe). Para ello cuentan con un conjunto de datos de entrenamiento:
codigoCliente: Identificación del cliente
sumValTot: Suma del valor transaccionado al mes
Frecuencia: Número de transacciones del mes
edad: Edad del cliente
estadoCivil: C: Casada, D: Divorciada, N & missing: Sin info, S: Soltera, U: Unida, V: viuda
nivelEducacion: missing o N: Sin info, P o S: primaria o secundaria, Sup: Superior
sexo: F: Femenino, M: Masculino
tipoVivienda: P: Propia, NP: No propia
nivelIngresos: Ingresos del cliente
Uafe 1: sospechosa, 0: no sospechosa
9.2.2.1. Paso 1: lectura de datos#
uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/refs/heads/master/challengeTrainUafe.csv"
datos = pd.read_csv(uu,sep = ",")
datos.describe()
| codigoCliente | sumValTot | Frecuencia | edad | nivelIngresos | Uafe | |
|---|---|---|---|---|---|---|
| count | 53871.000000 | 53871.000000 | 53871.000000 | 53871.000000 | 53871.000000 | 53871.000000 |
| mean | 330632.616937 | 2607.336492 | 13.792040 | 43.990559 | 1080.108966 | 0.049192 |
| std | 214567.625599 | 7885.583015 | 12.211262 | 14.429626 | 4759.779271 | 0.216270 |
| min | 1.000000 | 0.000000 | 1.000000 | 7.553425 | 0.000000 | 0.000000 |
| 25% | 40082.500000 | 251.045000 | 4.000000 | 32.531507 | 537.480000 | 0.000000 |
| 50% | 444937.000000 | 1528.440000 | 11.000000 | 40.238356 | 849.150000 | 0.000000 |
| 75% | 484662.000000 | 2430.470000 | 20.000000 | 51.857534 | 1186.490000 | 0.000000 |
| max | 570579.000000 | 342658.560000 | 148.000000 | 122.591781 | 849019.000000 | 1.000000 |
9.2.2.2. Paso 2: Separación de datos en entrenamieto y prueba#
# Importa la función train_test_split del módulo model_selection de scikit-learn
# Esta función permite dividir un conjunto de datos en subconjuntos de entrenamiento y prueba
from sklearn.model_selection import train_test_split
# Divide el DataFrame 'datos' en dos subconjuntos: entrenamiento (train_df) y prueba (test_df)
# El parámetro random_state=0 garantiza que la partición sea reproducible (misma división cada vez que se ejecuta)
train_df, test_df = train_test_split(datos, random_state=0)
9.2.2.3. Paso 3: Exploración de datos y selección de variables#
#pip install sweetviz
import sweetviz as sv
#my_report = sv.analyze(train_df)
my_report = sv.compare([train_df,'Train'],[test_df,'Test'],target_feat = 'Uafe')
my_report.show_html()
Report SWEETVIZ_REPORT.html was generated! NOTEBOOK/COLAB USERS: the web browser MAY not pop up, regardless, the report IS saved in your notebook/colab files.
9.2.2.4. Paso 4: Selección de variables#
# Importa dos funciones estadísticas de scipy:
# ks_2samp: para realizar la prueba de Kolmogorov-Smirnov entre dos muestras
# chi2_contingency: para realizar pruebas de chi-cuadrado en tablas de contingencia (no se usa aquí, pero está importada)
from scipy.stats import ks_2samp, chi2_contingency
# Comentario: Se realizará la prueba KS para comparar la distribución de variables continuas entre dos grupos definidos por la variable 'Uafe'
# Se crea un diccionario vacío para almacenar los resultados de la prueba KS para cada variable
ks_results = {}
# Se itera sobre las columnas numéricas seleccionadas
for column in ['sumValTot', 'Frecuencia', 'edad', 'nivelIngresos']:
# Se seleccionan los valores de la variable actual solo para el grupo Uafe == 0
group0 = train_df[train_df['Uafe'] == 0][column]
# Se seleccionan los valores de la variable actual solo para el grupo Uafe == 1
group1 = train_df[train_df['Uafe'] == 1][column]
# Se aplica la prueba de Kolmogorov-Smirnov para comparar si las dos muestras vienen de la misma distribución
ks_stat, ks_pvalue = ks_2samp(group0, group1)
# Se guardan el estadístico y el p-valor en el diccionario bajo el nombre de la variable
ks_results[column] = (ks_stat, ks_pvalue)
# Se imprime el diccionario con los resultados de la prueba KS para cada variable
ks_results
{'sumValTot': (0.17290718018142842, 1.0048834804337842e-49),
'Frecuencia': (0.11513715049095713, 3.254205628336455e-22),
'edad': (0.1312846698783937, 8.96037182115701e-29),
'nivelIngresos': (0.22921117173977315, 1.7264084511184317e-87)}
# Prueba de Chi-Cuadrado para variables categóricas
# Importante: esta prueba evalúa si existe una relación significativa entre dos variables categóricas
# Se crea un diccionario vacío para almacenar los resultados de cada variable
chi2_results = {}
# Se itera sobre cada una de las variables categóricas especificadas
for column in ['estadoCivil', 'nivelEducacion', 'sexo', 'tipoVivienda']:
# Se construye una tabla de contingencia que cruza cada categoría de la variable con los valores de 'Uafe'
contingency_table = pd.crosstab(train_df[column], train_df['Uafe'])
# Se aplica la prueba de chi-cuadrado sobre la tabla de contingencia
# Esta prueba devuelve: estadístico, p-valor, grados de libertad, y frecuencias esperadas
chi2_stat, chi2_pvalue, _, _ = chi2_contingency(contingency_table)
# Se almacenan el estadístico y el p-valor en el diccionario con el nombre de la variable como clave
chi2_results[column] = (chi2_stat, chi2_pvalue)
# Se imprime el diccionario con los resultados de la prueba de Chi-Cuadrado para cada variable categórica
chi2_results
{'estadoCivil': (76.6598679377394, 1.7466999003822897e-14),
'nivelEducacion': (65.9457747501759, 4.786928719287691e-15),
'sexo': (0.0, 1.0),
'tipoVivienda': (190.52545850499502, 2.441381309048441e-43)}
9.2.2.5. Paso 5: Entrenar un modelo con variables seleccionadas#
# Importa numpy para operaciones numéricas
import numpy as np
# Importa funciones para dividir los datos en entrenamiento y validación
from sklearn.model_selection import train_test_split
# Importa transformadores para escalar variables numéricas y codificar categóricas
from sklearn.preprocessing import StandardScaler, OneHotEncoder
# Permite aplicar distintos transformadores a diferentes columnas
from sklearn.compose import ColumnTransformer
# Permite encadenar pasos de procesamiento y modelado en un solo objeto
from sklearn.pipeline import Pipeline
# Importa el modelo de regresión logística
from sklearn.linear_model import LogisticRegression
# Importa métricas para evaluar el desempeño del modelo
from sklearn.metrics import roc_curve, roc_auc_score, classification_report, confusion_matrix
# Para generar gráficos (como la curva ROC)
import matplotlib.pyplot as plt
# ---------------------------------------------------------
# DEFINICIÓN DE VARIABLES INDEPENDIENTES Y DEPENDIENTE
# ---------------------------------------------------------
# Se seleccionan las variables predictoras (características) del DataFrame de entrenamiento
X = train_df[['sumValTot', 'Frecuencia', 'edad', 'nivelIngresos',
'estadoCivil', 'nivelEducacion', 'tipoVivienda']]
# Se define la variable objetivo (etiqueta a predecir)
y = train_df['Uafe']
# ---------------------------------------------------------
# DIVISIÓN EN CONJUNTOS DE ENTRENAMIENTO Y VALIDACIÓN
# ---------------------------------------------------------
# Se divide el conjunto de datos en entrenamiento y validación (80%-20%)
# El parámetro random_state=42 garantiza reproducibilidad
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2, random_state=42)
# ---------------------------------------------------------
# DEFINICIÓN DEL PREPROCESAMIENTO
# ---------------------------------------------------------
# Lista de características numéricas a escalar
numeric_features = ['sumValTot', 'Frecuencia', 'edad', 'nivelIngresos']
# Lista de características categóricas a codificar
categorical_features = ['estadoCivil', 'nivelEducacion', 'tipoVivienda']
# Se define un transformador de columnas:
# Escala las numéricas con StandardScaler y codifica las categóricas con OneHotEncoder
preprocessor = ColumnTransformer(
transformers=[
('num', StandardScaler(), numeric_features), # Escalamiento estándar
('cat', OneHotEncoder(), categorical_features) # Codificación one-hot
])
# ---------------------------------------------------------
# CREACIÓN DEL PIPELINE COMPLETO
# ---------------------------------------------------------
# Se construye un pipeline que primero preprocesa y luego aplica regresión logística
pipeline = Pipeline(steps=[
('preprocessor', preprocessor), # Paso 1: preprocesamiento
('classifier', LogisticRegression(max_iter=1000)) # Paso 2: modelo de clasificación
])
# ---------------------------------------------------------
# ENTRENAMIENTO DEL MODELO
# ---------------------------------------------------------
# Se entrena el pipeline completo con los datos de entrenamiento
pipeline.fit(X_train, y_train)
# ---------------------------------------------------------
# PREDICCIÓN Y PROBABILIDADES
# ---------------------------------------------------------
# Se generan predicciones finales (clase 0 o 1)
y_pred = pipeline.predict(X_val)
# Se generan probabilidades de pertenecer a la clase 1 (necesarias para curvas ROC)
y_pred_prob = pipeline.predict_proba(X_val)[:, 1]
Ahora vemos las probabilidades predichas:
#pd.DataFrame(y_pred).describe()
# Muestra un resumen estadístico (mínimo, percentiles, media, etc.)
# de las probabilidades predichas para la clase positiva (Uafe=1)
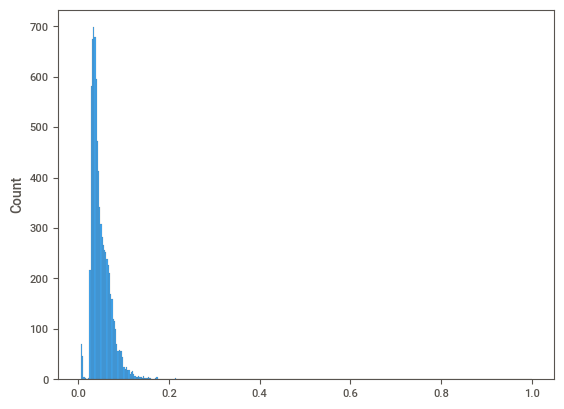
print(pd.DataFrame(y_pred_prob).describe())
# Importa la biblioteca Seaborn para visualización estadística
import seaborn as sns
# Genera un histograma para visualizar la distribución de las probabilidades predichas
# Esto ayuda a entender cuántos casos son clasificados con alta, media o baja probabilidad
sns.histplot(y_pred_prob)
0
count 8081.000000
mean 0.050014
std 0.025465
min 0.005897
25% 0.034214
50% 0.043393
75% 0.061111
max 0.999984
<Axes: ylabel='Count'>
# Calcular la curva ROC:
# fpr: tasa de falsos positivos
# tpr: tasa de verdaderos positivos
# thresholds: umbrales evaluados por el modelo para generar la curva
fpr, tpr, thresholds = roc_curve(y_val, y_pred_prob)
# Calcular el área bajo la curva ROC (AUC), que mide la capacidad predictiva global del modelo
roc_auc = roc_auc_score(y_val, y_pred_prob)
# ---------------------------------------------
# ENCONTRAR EL MEJOR UMBRAL (PUNTO DE CORTE)
# ---------------------------------------------
# Índice de Youden: J = Sensibilidad - (1 - Especificidad) = TPR - FPR
# El mejor umbral es aquel que maximiza esta diferencia
J = tpr - fpr
# Encuentra el índice del valor máximo de J
ix = np.argmax(J)
# Selecciona el mejor umbral correspondiente
best_threshold = thresholds[ix]
# ---------------------------------------------
# GRAFICAR LA CURVA ROC CON EL MEJOR PUNTO
# ---------------------------------------------
# Crea una nueva figura para graficar
plt.figure()
# Traza la curva ROC (TPR vs. FPR)
plt.plot(fpr, tpr, color='darkorange', lw=2,
label='Curva AUC (área = %0.2f)' % roc_auc)
# Línea diagonal que representa un modelo aleatorio (sin capacidad predictiva)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
# Dibuja el punto correspondiente al mejor umbral
plt.scatter(fpr[ix], tpr[ix], marker='o', color='black', label='Mejor Punto de Corte')
# Ajustes del gráfico
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('Tasa de Falsos Positivos')
plt.ylabel('Tasa de Verdaderos Positivos')
plt.title('Curva ROC')
plt.legend(loc="lower right")
# Muestra el gráfico
plt.show()
# Imprime el mejor umbral encontrado según el índice de Youden
print('Mejor punto de corte:', best_threshold)
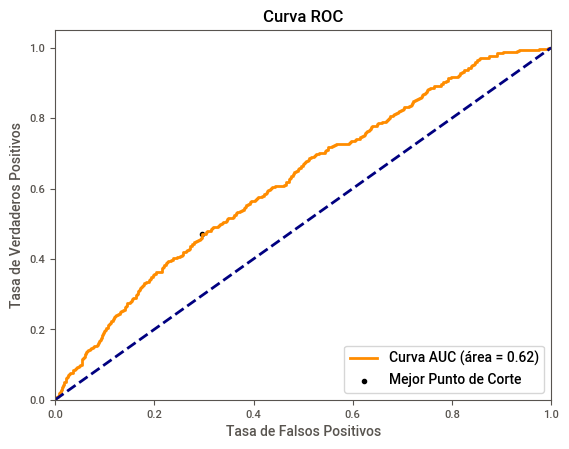
Mejor punto de corte: 0.056425144999863654
# -----------------------------------------------------
# GENERAR PREDICCIONES BINARIAS CON EL MEJOR UMBRAL
# -----------------------------------------------------
# Convierte las probabilidades en predicciones binarias (0 o 1)
# Si la probabilidad es mayor o igual al mejor umbral, se predice 1 (positivo), de lo contrario 0
predicciones_binarias = (y_pred_prob >= best_threshold).astype(int)
# -----------------------------------------------------
# REPORTE DE CLASIFICACIÓN
# -----------------------------------------------------
# Genera un reporte con métricas de evaluación:
# Precisión (precision), sensibilidad (recall), F1-score y soporte por clase
classification_rep = classification_report(y_val, predicciones_binarias)
# -----------------------------------------------------
# MATRIZ DE CONFUSIÓN
# -----------------------------------------------------
# Crea la matriz de confusión: compara etiquetas reales vs. predichas
# Devuelve: [[TN, FP], [FN, TP]]
conf_matrix = confusion_matrix(y_val, predicciones_binarias)
#Imprimir la linea devuelve el area bajo la curva ROC, reporte de clasificacion y la matriz de confusión
print("AUC:",roc_auc,"\n")
print("Matriz de confusión\n",conf_matrix,"\n")
print("Reporte de clasificación\n",classification_rep,"\n")
AUC: 0.6221461259050277
Matriz de confusión
[[5424 2286]
[ 196 175]]
Reporte de clasificación
precision recall f1-score support
0 0.97 0.70 0.81 7710
1 0.07 0.47 0.12 371
accuracy 0.69 8081
macro avg 0.52 0.59 0.47 8081
weighted avg 0.92 0.69 0.78 8081
Ahora se genera la tabla de ganancias (también llamada tabla de validación o lift table) para train y test, usando los deciles del score predicho (y_pred_prob en test y el equivalente en train). Incluirá:
Total de observaciones por decil
Total de “malos” (Uafe = 1)
Total de “buenos” (Uafe = 0)
Razón de malos
Porcentaje acumulado de malos (captura acumulada)
def generar_tabla_ganancias(y_true, y_prob, n_deciles=10):
# Crear DataFrame con los datos reales y probabilidad predicha
df = pd.DataFrame({'real': y_true, 'score': y_prob})
# Crear deciles (del 1 al n_deciles), 1 es el más riesgoso (score más alto)
df['decil'] = pd.qcut(df['score'], q=n_deciles, labels=False, duplicates='drop')
df['decil'] = n_deciles - df['decil'] # Invertir para que 1 sea el más riesgoso
# Agrupar por decil
tabla = df.groupby('decil').agg(
total=('real', 'count'),
malos=('real', 'sum')
).reset_index()
# Calcular buenos, razón de malos, y acumulados
tabla['buenos'] = tabla['total'] - tabla['malos']
tabla['razon_malos'] = tabla['malos'] / tabla['total']
tabla['malos_acum'] = tabla['malos'].cumsum()
tabla['porc_malos_acum'] = 100 * tabla['malos_acum'] / tabla['malos'].sum()
return tabla
# Aplicar para TRAIN
y_train_prob = pipeline.predict_proba(X_train)[:, 1]
tabla_train = generar_tabla_ganancias(y_train, y_train_prob)
# Aplicar para TEST
tabla_test = generar_tabla_ganancias(y_val, y_pred_prob)
print("Tabla de Ganancias - TRAIN")
print(tabla_train)
Tabla de Ganancias - TRAIN
decil total malos buenos razon_malos malos_acum porc_malos_acum
0 1 3233 314 2919 0.097123 314 19.503106
1 2 3232 246 2986 0.076114 560 34.782609
2 3 3232 180 3052 0.055693 740 45.962733
3 4 3232 163 3069 0.050433 903 56.086957
4 5 3232 147 3085 0.045483 1050 65.217391
5 6 3232 137 3095 0.042389 1187 73.726708
6 7 3232 155 3077 0.047958 1342 83.354037
7 8 3232 155 3077 0.047958 1497 92.981366
8 9 3232 83 3149 0.025681 1580 98.136646
9 10 3233 30 3203 0.009279 1610 100.000000
print("Tabla de Ganancias - TEST")
print(tabla_test)
Tabla de Ganancias - TEST
decil total malos buenos razon_malos malos_acum porc_malos_acum
0 1 808 68 740 0.084158 68 18.328841
1 2 808 60 748 0.074257 128 34.501348
2 3 808 41 767 0.050743 169 45.552561
3 4 808 37 771 0.045792 206 55.525606
4 5 808 38 770 0.047030 244 65.768194
5 6 808 27 781 0.033416 271 73.045822
6 7 808 33 775 0.040842 304 81.940701
7 8 808 35 773 0.043317 339 91.374663
8 9 808 26 782 0.032178 365 98.382749
9 10 809 6 803 0.007417 371 100.000000
9.3. Probit#
En los modelos logia se propuso la logística, en este caso se propone la Función de Distribución Acumulada Normal. Suponga que la variable de respuesta es binaria, 1 o 0. \(Y\) podría representar la presencia/ausencia de una condición, éxito/fracaso, si/no. Se tiene también un vector de regresoras \(X\), el modelo toma la forma:
\[
{\displaystyle \Pr(Y=1\mid X)=\Phi (X^{T}\beta ),}
\]
donde \(Pr\) es la prbabilidad y \(\Phi\) distribución acumulada de la normal estándar \({\displaystyle \Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt}\). Los parámetros \(\beta\) se estiman típicamente con el método de máxima verosimilitud.
Ejemplo
uu = "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/GA/tabla15_7.csv"
datos = pd.read_csv(uu,sep = ';')
ajuste1 = smf.probit('GRADE ~ GPA + TUCE + PSI',data = datos).fit()
print(ajuste1.summary())
Optimization terminated successfully.
Current function value: 0.400588
Iterations 6
Probit Regression Results
==============================================================================
Dep. Variable: GRADE No. Observations: 32
Model: Probit Df Residuals: 28
Method: MLE Df Model: 3
Date: Wed, 04 Jun 2025 Pseudo R-squ.: 0.3775
Time: 06:05:30 Log-Likelihood: -12.819
converged: True LL-Null: -20.592
Covariance Type: nonrobust LLR p-value: 0.001405
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept -7.4523 2.542 -2.931 0.003 -12.435 -2.469
GPA 1.6258 0.694 2.343 0.019 0.266 2.986
TUCE 0.0517 0.084 0.617 0.537 -0.113 0.216
PSI 1.4263 0.595 2.397 0.017 0.260 2.593
==============================================================================
ajuste1.get_margeff(at='mean').summary()
| Dep. Variable: | GRADE |
|---|---|
| Method: | dydx |
| At: | mean |
| dy/dx | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| GPA | 0.5333 | 0.232 | 2.294 | 0.022 | 0.078 | 0.989 |
| TUCE | 0.0170 | 0.027 | 0.626 | 0.531 | -0.036 | 0.070 |
| PSI | 0.4679 | 0.188 | 2.494 | 0.013 | 0.100 | 0.836 |
mm = ajuste1.get_margeff(at='all').margeff
mm[0:10,:]
array([[0.07255307, 0.00230845, 0.06365122],
[0.17584323, 0.00559486, 0.15426826],
[0.44108314, 0.01403409, 0.38696473],
[0.07391114, 0.00235166, 0.06484266],
[0.64252589, 0.02044346, 0.5636916 ],
[0.10206861, 0.00324755, 0.08954537],
[0.07368267, 0.00234439, 0.06464222],
[0.15292232, 0.00486558, 0.13415961],
[0.3033272 , 0.00965106, 0.26611067],
[0.59359928, 0.01888675, 0.520768 ]])
ajuste1.predict(which = 'linear')
array([-2.09308603, -1.61569183, -0.87816803, -2.08420699, 0.13722837,
-1.92311086, -2.08569187, -1.69993698, -1.23289159, 0.42099513,
-2.14186033, -0.86486457, -0.45841206, -0.85895528, -0.36825763,
-2.01475018, -1.6881184 , -1.86842727, 0.23630576, 0.40479606,
-1.53878182, 1.30785551, -0.60319106, 1.02555852, 0.97087493,
-0.02826337, 0.3649008 , -0.44357981, 0.99452719, 1.6670186 ,
0.10033167, -1.15745135])