4. Estadística Descriptiva

• Librería básica: scipy.stats (importado como stats)

• SciPy es una biblioteca de computación científica que utiliza NumPy como base.

• SciPy significa Scientific Python.

• Proporciona más funciones de utilidad para optimización, álgebra lineal, funciones especiales, procesamiento de señales, entre otras.

• Al igual que NumPy, SciPy es de código abierto, por lo que podemos usarlo libremente.

• SciPy fue creado por el creador de NumPy, Travis Olliphant.

4.1. Medidas de resumen

4.1.1. Medidas de tendencial central

Creamos 100 números aleatorios con distribución normal:

import numpy as np
N = 100
np.random.seed(85) # genera una semilla para los números aleatorios
x = np.random.normal(loc = 0, scale = 1, size = N)

4.1.1.1. Promedio

Promedio o media: notado como \(\bar{x}\), de un conjunto de \(n\) datos \(x_1,x_2,\ldots,x_n\) es igual a la suma de valores dividido para \(n\).

\[ \bar{x} = \frac{x_1+x_2+\ldots+x_n}{n}=\frac{\sum_{i=1}^nx_i}{n} \]

• Si las observaciones están agrupadas en una tabla de frecuencia de datos individuales de \(k\) valores, el promedio se calcula

\[ \bar{x} =\frac{\sum_{i=1}^kn_ix_i}{n} \]

donde \(n = {\sum_{i=1}^kn_i}\).

• Si las observaciones están agrupadas en una tabla de frecuencias agrupadas por clases, se calcula el punto promedio de cada clase \(x_i = \frac{l_i+s_i}{2}\) (\(i = 1,2,\ldots,k\)), donde \(l_i\) y \(s_i\) son la cota inferior y superor de cada clase respectivamente. El promedio es

\[ \bar{x} =\frac{\sum_{i=1}^kn_ix_i}{n} \]

Ventajas y desventajas del promedio:

• Se expresan en las mismas unidades quela variable

• En su cálculo intervienen todos los valores de la distribución

• Es el centro de gravedad de toda la distribución

• Es único

• Su principal inconveniente es que se ve afectado por valores atípicos

np.mean(x)

-0.07448679690601528

Toma en cuenta lo que pasa con valores nan. hstack agrega valores al vector:

x1 = np.hstack((x,np.nan))

np.mean(x1)

nan

np.nanmean(x1)

-0.07448679690601528

np.nanstd(x1)

1.0336795016636526

np.nanvar(x1)

1.0684933121596172

np.median(x)

-0.15334269473584197

4.1.1.2. Mediana

La mediana de un conjunto de datos \(x_1+x_2+\ldots+x_n\) es el valor que se encuentra en el punto medio, cuando se ordenan los valores de menor a mayor.

Se nota como \(Q_2\) o Med y tiene la propiedad de que a cada lado se encuentra el 50% de los datos.

Ventajas:

• No se ve afectada por valores extremos o atípicos

• Fácil de interpretar como el “valor medio” de un conjunto de datos. Divide los datos en dos mitades.

• En distribuciones asimétricas, la mediana proporciona una mejor representación del centro que la media, ya que no se ve arrastrada hacia la cola de la distribución.

Desventajas:

• La mediana es menos sensible a los cambios en los valores de los datos individuales en comparación con la media.

• A diferencia de la media, la mediana no toma en cuenta todos los valores del conjunto de datos, sino solo el valor central.

np.median(x)

-0.15334269473584197

4.1.1.3. La moda

Es el valor que más se repite en un conjunto de datos.

Ventajas:

• Fácil de entender y calcular, especialmente en conjuntos de datos pequeños o cuando se analizan datos categóricos.

• Única medida de tendencia central que puede aplicarse a datos cualitativos o categóricos, como colores, marcas o tipos

• La moda no se ve influenciada por valores atípicos o extremos.

Desventajas:

• Puede haber más de una moda (multimodal), lo que complica la interpretación.

• La moda no siempre representa bien el centro de la distribución, especialmente en distribuciones con una moda que es significativamente diferente de la media o la mediana.

• Para datos continuos, la moda es menos útil, ya que cada valor puede ser único o tener una baja frecuencia, dificultando la identificación de una moda clara.

from scipy import stats

data = [5,3,7,7,9,7]

stats.mode(data)

ModeResult(mode=7, count=3)

Cuando tenemos resultados en varios elementos como el anterior (mode=7, count=3), podemos guardarlos de la siguiente manera:

(valor, freq) = stats.mode(data)
(valor, freq)

(7, 3)

4.1.2. Medidas de Dispersión

4.1.2.1. Rango

Diferencia entre el valor más alto y el valor más bajo

Ventajas:

• Fácil de calcular y comprender.

• Proporciona una idea rápida de la amplitud de los datos, lo que puede ser útil para comparar la variabilidad entre diferentes conjuntos de datos.

Desventajas:

• El rango se ve afectado por los valores atípicos, ya que depende únicamente de los valores máximo y mínimo. Un solo valor extremo puede distorsionar significativamente el rango.

• Dos conjuntos de datos con el mismo rango pueden tener distribuciones internas muy diferentes.

En Python se usa la función np.ptp donde ptp significa peak to peak

range = np.ptp(x)

range

4.142508144337905

4.1.2.2. Desviación estándar

Fue introducida por Karl Person en 1894 y se define:

La desviación estándar (o desviación típica), notada por \(s\), de un conjunto de \(n\) mediciones \(x_1+x_2+\ldots+x_n\) es la raíz cuadrada de las desviaciones de las mediciones, respecto al promedio \(\bar{x}\), dividida entre \(n-1\); es decir

\[ s = \sqrt{\frac{1}{n-1}\sum_{i = 1}^{n}(x_i-\bar{x})^2} \]

• Se expresa en las mismas unidades que los datos originales

• En su cálculo intervienen todos los valores de la distribución

• Es única

• Se ve afectada por valores atípicos

np.std(x)

1.0336795016636526

4.1.2.3. Varianza

np.var(x)

1.0684933121596172

4.1.2.4. Cuantiles

Un cuantil divide la distribución de los datos en una proporción específica, el cuantil es el dato que corresponde a dicha división.

El cuantil de orden \(p\) de una distribución (con \(0 < p < 1\)) es el valor de la variable \(x_{p}\) que marca un corte de modo que una proporción \(p\) de valores de la población es menor o igual que \(x_{p}\). Por ejemplo, el cuantil de orden \(0.36\) dejaría un 36% de valores por debajo y el cuantil de orden \(0.50\) se corresponde con la mediana de la distribución.

Los cuantiles suelen usarse por grupos que dividen la distribución en partes iguales; entendidas estas como intervalos que comprenden la misma proporción de valores. Los más usados son:

• Los cuartiles, que dividen a la distribución en cuatro partes (corresponden a los cuantiles \(0.25\); \(0.50\) y \(0.75\));

• Los quintiles, que dividen a la distribución en cinco partes (corresponden a los cuantiles \(0.20\); \(0.40\); \(0.60\) y \(0.80\));

• Los deciles, que dividen a la distribución en diez partes;

• Los percentiles, que dividen a la distribución en cien partes.

from scipy import stats

#https://docs.scipy.org/doc/scipy/reference/stats.html
stats.mstats.mquantiles(x)

array([-0.97667604, -0.15334269,  0.70789384])

stats.mstats.mquantiles(x,prob=np.arange(0,1.1,0.1))

array([-1.76475402, -1.38045444, -1.05285905, -0.76411302, -0.49263867,
       -0.15334269,  0.16959572,  0.45482   ,  0.92681765,  1.44781882,
        2.37775412])

stats.describe(x)

DescribeResult(nobs=100, minmax=(-1.7647540193678475, 2.3777541249700573), mean=-0.07448679690601528, variance=1.0792861738986033, skewness=0.3655289306119107, kurtosis=-0.7791352022265521)

4.2. Distribuciones

4.2.1. Variables aleatorias (v.a.)

• Una variable aleatoria es un resultado numérico de un experimento.

• Las variables aleatorias que estudiamos tienen dos variantes: discretas or continuas.

• Las v.a discretas son las que tienen un número contable de posibilidades.

  • \(P(X = k)\)

• Las v.a. continuas toman valores en los reales o un subconjunto de los reales.

  • \(P(X \in A)\)

---

4.2.2. Ejemplos de v.a.

• Los resultados \((0-1)\) del lanzamiento de una moneda

• Los resultados del lanzamiento de un dado

• El índice de masa corpotal de una persona en una toma futura a la línea base

• El estado de hipertensión de una persona seleccionada al alzar de una población

---

4.2.3. Función de masa de probabilidad \(p(x)\)

Una función de masa de probabilidad evaluada en un valor corresponde a la probabilidad que una v.a. toma ese valor. Para se una función válida, se debe satisfacer:

1. \(p(x) \geq 0\) for all \(x\)

2. \(\sum_{x} p(x) = 1\)

La suma se toma sobre todos los valores de \(x\).

---

4.2.3.1. Ejemplo

Sea \(X\) el resultado del lanzamiento de una moneda donde \(X=0\) representa sello y \(X = 1\) representa cara. $\( p(x) = (1/2)^{x} (1/2)^{1-x} ~~\mbox{ for }~~x = 0,1 \)\( Suponga que no sabemos si la moneda es justa. Sea \)\theta\( la probabilidad de que salga cara se expresa como una proporción (entre 0 y 1). \)\( p(x) = \theta^{x} (1 - \theta)^{1-x} ~~\mbox{ for }~~x = 0,1 \)$

---

4.2.4. Función de densidad

Una función de densidad (pdf), es una función asociada con una v.a. continua

Las areas debajo las pdfs corresponden a las probabilidades de esa v.a.

La función \(f\) debe satisfacer

1. \(f(x) \geq 0\) para todo \(x\)

2. El área debajo de \(f(x)\) es uno.

---

4.2.4.1. Ejemplo

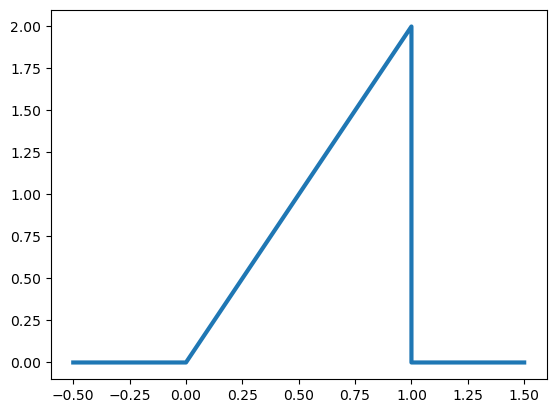
Supongamos que la proporción de llamadas de ayuda que se atienden en un día aleatorio en una línea de ayuda está dada por

\[\begin{split} f(x) = \left\{\begin{array}{ll} 2 x & \mbox{ para } 1 > x > 0 \\ 0 & \mbox{ en otro caso} \end{array} \right. \end{split}\]

¿Es esta una densidad válida?

---

import matplotlib.pyplot as plt

x = [-0.5, 0, 1, 1, 1.5]
y = [0, 0, 2, 0, 0]

plt.plot(x, y, linewidth=3)

[<matplotlib.lines.Line2D at 0x7fd0a961a5b0>]

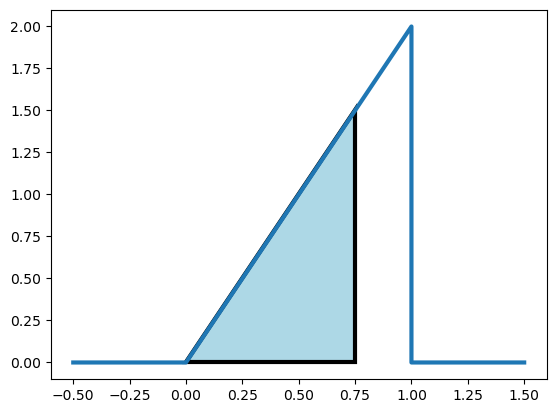
4.2.4.2. Ejemplo

¿Cuál es la probabilidad de que se atienda el 75% o menos de las llamadas?

import matplotlib.pyplot as plt

# Datos para la línea
x = [-0.5, 0, 1, 1, 1.5]
y = [0, 0, 2, 0, 0]

# Crear la figura y los ejes
fig, ax = plt.subplots()

# Dibujar la línea
ax.plot(x, y, linewidth=3)

# Dibujar el polígono
polygon_x = [0, 0.75, 0.75, 0]
polygon_y = [0, 0, 1.5, 0]
ax.fill(polygon_x, polygon_y, color="lightblue", linewidth=3, edgecolor="black")

[<matplotlib.patches.Polygon at 0x7fd0a9924340>]

from scipy.stats import beta

result_pbeta = beta.cdf(0.75, 2, 1)
print(1.5 * .75 / 2)
print(result_pbeta)

0.5625
0.5625

4.2.5. Función de distribución acumulada

• La función de distribución acumulada (CDF) de una v.a. \(X\) se define como la función $\( F(x) = P(X \leq x) \)$

• Esta definición aplica indistintamente de si \(X\) es discreta o continua.

• La función de supervivencia de una v.a. \(X\) es definida como

\[ S(x) = P(X > x) \]

• Note que \(S(x) = 1 - F(x)\)

• Para v.a. continuas, la función de densidad es la derivada de la acumulada

---

4.2.5.1. Ejemplo

¿Cuál es la función de supervivencia y CDF de la densidad considerada antes?

Para \(1 \geq x \geq 0\) $\( F(x) = P(X \leq x) = \frac{1}{2} Base \times Height = \frac{1}{2} (x) \times (2 x) = x^2 \)$

\[ S(x) = 1 - x^2 \]

print(beta.cdf([0.4, 0.5, 0.6], 2, 1))

[0.16 0.25 0.36]

4.2.6. Función Cuantil

• La función cuantil (QF) de una v.a. \(X\) se define como la función $\( Q(x) = F^{-1}(x) \)$

Es decir, la función cuantil es la inversa de la función de distribución acumulada.

4.2.7. En Python

miFD = stats.norm(5,3)

miFD

<scipy.stats._distn_infrastructure.rv_continuous_frozen at 0x7fd0a9973280>

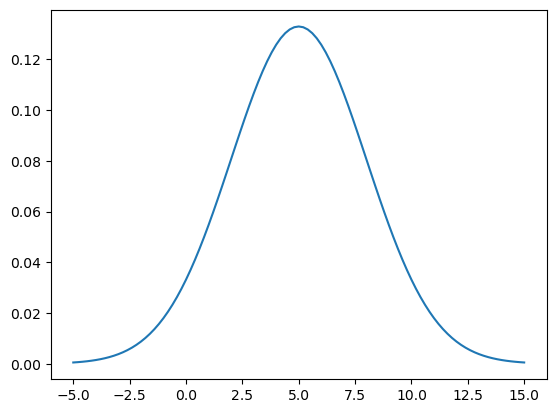
x = np.linspace(-5,15,101)
y1 = miFD.pdf(x) # densidad
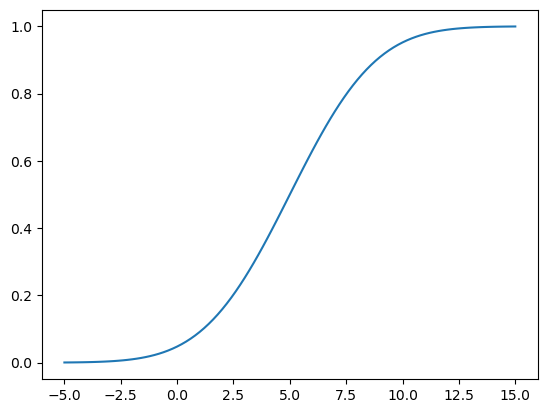
y2 = miFD.cdf(x) # acumulada
y3 = miFD.ppf(y2) # cuantil

import matplotlib.pyplot as plt

plt.figure()
plt.plot(x,y1,'-');

plt.figure()
plt.plot(x,y2,'-');

plt.figure()
x1 = np.linspace(0,1, len(y3))
plt.plot(y2,y3,'-');

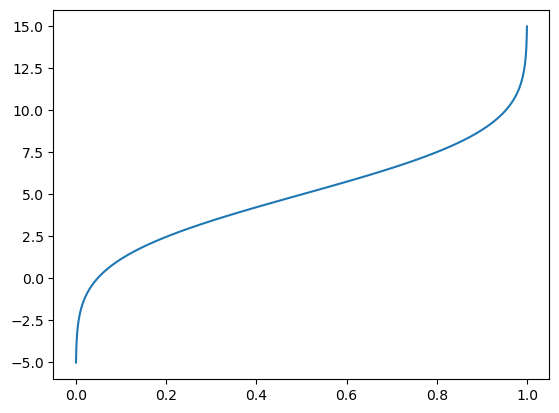
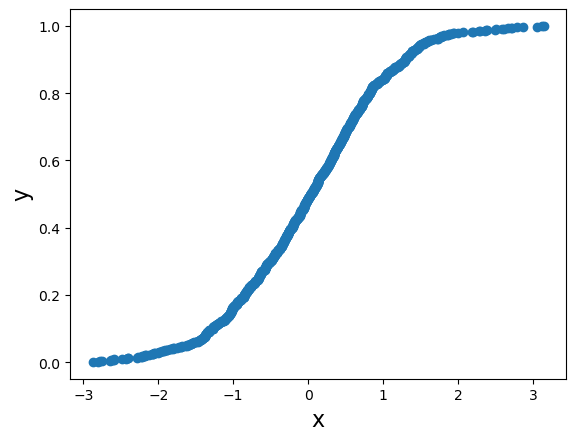
Distribución acumulada empírica

x = stats.norm.rvs(loc=0,scale=1,size=1000) # distribucion normal estandar
x = np.sort(x) # odenamos los valores de la variable
n = x.size # tamano de la muestra
y = np.arange(1, n+1) / n # % acumulado

plt.figure()
plt.scatter(x=x, y=y);
plt.xlabel('x', fontsize=16)
plt.ylabel('y', fontsize=16)

Text(0, 0.5, 'y')

from statsmodels.distributions.empirical_distribution import ECDF
ecdf = ECDF(x)

ecdf(1.5)

0.9440000000000001

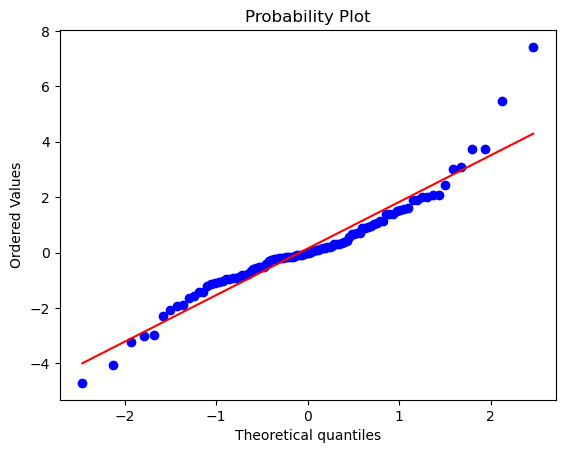
QQ plot

#https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.probplot.html#scipy.stats.probplot
nsample = 100
np.random.seed(7654321)

plt.figure()
x = stats.t.rvs(df=3, size=nsample)
res = stats.probplot(x, plot=plt)